Die Mühen, die für die verschiedenen Bereiche der mathematischen Wissenschaften auf zu wenden sind, können, obwohl sie auf den ersten Blick Aufgaben allein für den Intellekt zu sein scheinen, dennoch in zwei grundverschiedene Gebiete unterteilt werden. Als das eine Gebiet wäre das mechanische zu nennen, welches präzisen und unveränderlichen Gesetzen unterliegt, deren Bedeutung mit methodischen Abläufen in Geräten darstellbar ist. Das zweite Gebiet liegt im Bereich des Verstandes, da es den Eingriff des Denkens erfordert. Nachdem wir dies verstanden haben, können wir daran gehen, den mechanischen Zweig der Bemühungen von Automaten erledigen zu lassen und dem Intellekt den Part zukommen lassen, welcher der Fähigkeit des Denkens bedarf. Die starre Exaktheit der Gesetze, in denen die Regeln numerischer Berechnungen festgelegt sind, haben sicherlich schon vielfach die Idee nahe gelegt, für die Gesamtheit solcher Berechnungen, oder zur Erleichterung von Teilberechnungen, passende Instrumente zu verwenden. Es gab demnach auch viele Erfindungen mit diesem Ziel vor Augen, doch wurde es immer wieder nur teilweise erreicht. So ist die viel bewunderte Maschine von Pascal nur mehr ein Kuriosum, da sie, obwohl sie den großen Geist ihres Erfinders zeigt, nur sehr wenig praktischen Nutzen in sich birgt. Ihre Fähigkeiten beschränkten sich auf die Ausführung der vier Grundrechenarten der Arithmetik und sie war praktisch auf die ersten beiden beschränkt, da nur durch eine Serie von Additionen oder Subtraktionen das Endergebnis einer Multiplikation oder Division zu erhalten war. Der bisherige Hauptnachteil der meisten solcher Automaten lag darin, dass sie fortwährende Eingriffe eines menschlichen Betreibers benötigten, der ihre Bewegungen steuerte und der daher gleichzeitig eine Fehlerquelle darstellte. So liegt also der Grund dafür, dass diese Automaten nicht weithin bei aufwendigen numerischen Berechnungen eingesetzt werden, vor allem darin, dass sie nicht tatsächlich das gestellte doppelte Problem lösen, wie die Korrektheit der Ergebnisse bei gleichzeitig geringem Zeitaufwand gesichert werden könnte.
Von ähnlichen Gedanken betroffen hat Mr. Babbage einige Jahre auf die Realisierung einer gigantischen Idee verwandt. Er gab sich selbst keinen geringeren Auftrag als den, einen Automaten zu konstruieren, der nicht nur arithmetische Berechnungen ausführen sollte, sondern jede Art von analytischen Rechnungen, deren Gesetzmäßigkeiten bekannt sind. Eine solche Unternehmung scheint die Vorstellung im ersten Moment zu überfordern, doch wird bei längerer und ruhiger Betrachtung eine erfolgreiche Lösung der Aufgabe immer wahrscheinlicher und es stellt sich das Gefühl ein, dass dazu die Entdeckung eines grundlegenden Prinzips notwendig sein könnte, das den Automaten in die Lage versetzen müsste, mechanische Übersetzungen der ihm in algebraischer Notation gestellten Aufgaben auszuführen. Der illustre Erfinder war freundlich genug, mir einige seiner Einsichten zu diesem Thema während eines Besuchs in Turin mitzuteilen. Ich habe mit seiner Zustimmung die Eindrücke zusammengestellt, die diese Einsichten bei mir hinterlassen haben. Der Leser sollte nicht erwarten, eine Beschreibung von Mr. Babbages Maschine vorzufinden - diese zu verstehen würde langwierige Studien voraussetzen - ich will mich vielmehr bemühen, einen Ausblick auf die erzielbaren Ergebnisse zu geben und die Prinzipien darzulegen, auf denen die Erreichung dieser Ziele fußt.
Ich muss zunächst voraus schicken, dass diese Maschine völlig abweichend von derjenigen ist, die in dem "Traktat über die Wirtschaftlichkeit von Maschinen" desselben Autors erwähnt wird. Da aber letztere den Anstoß zur Idee ersterer gab, halte ich es für nützlich, zunächst einen kurzen Rückblick auf Mr. Babbages frühere Aufsätze und auf die Umstände, unter denen sie entstanden, zu werfen.
Es ist wohl bekannt, dass die französische Regierung, angeleitet von dem Wunsch, das Dezimalsystem zu verbreiten, die Erstellung enorm umfangreicher Tabellen der Logarithmen und der trigonometrischen Werte in Auftrag gab. M. de Prony, der mit der Leitung dieser Unternehmung beauftragt wurde, unterteilte die Aufgabe in drei Bereiche, in denen jeweils Personen mit speziellen Fähigkeiten beschäftigt wurden. Die erste Sektion kombinierte Formeln und stellte sie so um, dass sie numerischen Berechnungen zugänglich wurden. Die zweite Sektion errechnete dann für just diese Formeln die Ergebnisse für in ausgewählten, aufeinander folgenden Abständen liegende Werte der Variablen. Die dritte aus etwa 80 Personen bestehende Sektion, welche überwiegend nur die beiden ersten Grundrechenarten der Arithmetik beherrschten, berechnete schließlich weitere interpolierte Ergebnisse durch einfache Addition und Subtraktion der Ergebnisse der zweiten Sektion.
Als eine Unternehmung ganz ähnlich der eben erwähnten in England in Angriff genommen werden sollte, dachte Mr. Babbage darüber nach, wie die Arbeiten der dritten Sektion von einer Maschine ausgeführt werden könnten und er realisierte diese Idee durch einen Mechanismus, den er teilweise fertig stellte und der den Namen Differenzmaschine wegen eines Prinzips trug, das seiner Konstruktion zu Grunde lag. Um eine Vorstellung dieses Mechanismus zu vermitteln genügt es, sich die Abfolge der ganzen Quadratzahlen ins Gedächtnis zu rufen: 1, 4, 9, 16, 25, 36, 49, 64 &c. Durch Subtraktion jeder dieser Zahlen von der ihr nachfolgenden Zahl erhalten wir eine neue Abfolge, die wir die Folge der Ersten Differenzen nennen wollen. Sie besteht aus den Zahlen: 3, 5, 7, 9, 11, 13, 15 &c. Wenn wir in dieser Abfolge wiederum von jeder Zahl ihre Vorgängerin subtrahieren, erhalten wir die Folge der Zweiten Differenzen, die nun alle konstant gleich 2 sind. Wir können diese Abfolge von Operationen und ihre Ergebnisse in der folgenden Tabelle darstellen.
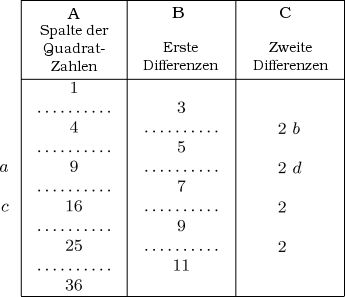
Aus der Art, wie die beiden rechten Spalten B und C formatiert sind, lässt sich leicht ersehen, dass, wenn wir etwa von der Zahl 5 zur folgenden 7 gelangen wollen, wir zur ersten Zahl die konstante Differenz 2 addieren müssen. In gleicher Weise müssen wir, wenn wir von der Quadratzahl 9 zur folgenden Quadratzahl 16 gelangen wollen, die Differenz 7 addieren, die mit anderen Worten die vorhergehende Differenz 5 plus der konstanten Differenz 2 ist. Oder wir müssen nur, noch einmal anders ausgedrückt, was aber dasselbe meint, um die Zahl 16 zu erhalten lediglich die drei Zahlen 2, 5 und 9 addieren, die auf der Achse ab liegen. Ähnlich erhalten wir die Zahl 25, wenn wir die drei Zahlen der Achse cd addieren. Durch die Addition von 2+7 erhielten wir die erste Differenz 9, die auf die 7 folgt. Addieren wir 16 zu der 9, dann erhalten wir die Quadratzahl 25. Wir sehen also, dass wenn nur die drei Zahlen 2, 5 und 9 gegeben sind, die ganze Serie der aufeinander folgenden Quadratzahlen, ebenso wie die Serie der Ersten Differenzen, durch das Ausführen simpler Additionen zu erhalten sind.
Um nun zu verstehen, wie diese Rechenoperationen von einem Automaten reproduziert werden könnten, nehmen sie eine Maschine an, die aus drei Skalenscheiben mit den Bezeichnungen A, B und C bestünde, deren jeweilige Unterteilung in, beispielsweise, tausend Markierungen mit einer Nadel abtastbar wäre. Die beiden Skalenscheiben C und B würden zusätzlich über einen Registrierhammer verfügen, der genau die Anzahl von Schlägen ausführen soll, die von der durch die Nadel seiner Skalenscheibe angezeigten Markierung vorgegeben sind. Für jeden Schlag des Registrierhammers von Skalenscheibe C soll sich nun die Nadel von B um eine Markierung weiterbewegen. In ähnlicher Weise soll die Nadel A um jeweils eine Markierung voranschreiten, wenn der Schlag des Hammers von Skalenscheibe B sie trifft. So die generelle Beschreibung der Art des Mechanismus.
Nachdem wir dieses Prinzip verstanden haben, lassen sie uns zu Beginn einer Serie von Operationen, die wir nun ausführen wollen, die Nadel der Skalenscheibe C auf die Markierung 2 stellen, die Nadel B auf die Markierung 5 und die Nadel A auf die Markierung 9. Lassen wir den Registrierhammer der Skalenscheibe C nun schlagen, so wird er dies zweimal tun und zur selben Zeit wird die Nadel der Skalenscheibe B um 2 Positionen vorrücken. Letztere wird dann die Zahl 7 anzeigen, die auf die Zahl 5 in der Spalte der ersten Differenzen folgt. Wenn wir anschließend den Hammer der Skalenscheibe B schlagen lassen, wird die Nadel der Skalenscheibe A sieben Schläge registrieren und somit um sieben Markierungen weiter rücken. Diese 7 addiert zu der Zahl 9, die zuvor auf der Skalenscheibe markiert war, wird die Zahl 16 ergeben, welches die nächste auf 9 folgende Quadratzahl ist. Wenn wir alle diese Operationen beginnend mit der Nadel C, die unverändert auf der Markierung 2 stehen bleibt, nun noch einmal starten, so werden wir durch Wiederholungen nach und nach die Folge der ganzen Quadratzahlen durch einen sehr einfachen Mechanismus produzieren.
Das Theorem, auf dem die Konstruktion der eben beschriebenen Maschine beruht, ist ein spezieller Fall des folgenden, generelleren Theorems: In einem beliebigen Polynom mit m als der höchsten Potenz der Variablen, werde diese Variable in gleichmäßigen Schritten erhöht, die zugehörigen Werte des Polynoms werden errechnet und die ersten, zweiten, dritten &c Differenzen der Ergebniswerte gebildet (so, wie in der vorangegangenen Folge der Quadrate), die m. Differenzen werden alle denselben Wert haben. Um nun die Abfolge der Ergebniswerte des Polynoms durch einen Automaten errechnen zu lassen, der dem beschriebenen gleicht, genügt es, wenn dieser Automat über (m+1) Skalenscheiben verfügt, die in vorherigem Beispiel beschriebener Weise aufeinander einwirken. Da die Differenzen sowohl positiv, als auch negativ sein können, böte der Automat die Möglichkeit, jede Nadel entweder vor- oder rückwärts zu bewegen, abhängig vom positiven oder negativen Vorzeichen der auszuführen algebraischen Addition.
Wenn wir von einem Polynom übergehen zu einer Serie mit einer unendlichen Anzahl von Termen, in der die Potenzen der Variablen in aufsteigender Folge erscheinen, dann scheint es zunächst so, dass ein zur Berechnung dieser Funktion geeigneter Automat auch eine unendliche Anzahl von Skalenscheiben haben müsste, was ihn praktisch unrealisierbar machen würde. In vielen Fällen wird diese Schwierigkeit aber verschwinden, da wir für eine große Menge von Funktionen beobachten können, dass die sie repräsentierenden Serien eine Konvergenz zeigen; daher können wir uns für eine Näherung der Lösungen, die wir wünschen, die Berechnung auf eine bestimmte Anzahl von Termen der Serie beschränken und den Rest ignorieren können. Durch diese Methode wird die Frage auf den einfachen Fall eines Polynoms mit einer geringen Anzahl von Gliedern begrenzt. Deshalb können wir so auch die Abfolge der Logarithmen von Zahlen errechnen. Nun ist es aber so, dass in diesem speziellen Fall die Skalenscheiben um so schnell ansteigende Werte erhöht werden, dass der Grad der Näherung davon unweigerlich beeinflusst wäre. Dies nötigt uns, in bestimmten Abständen den Wert der Funktion mit anderen Methoden zu errechnen und die Ergebnisse dieser Rechnungen jeweils als Startwerte für eine Folge von weiteren Zwischenwerten vorzugeben, die der Automat errechnen soll. Wir sehen also, dass der Automat die Aufgaben der dritten Abteilung der Berechnungen, die im Abschnitt über die von der französischen Regierung in Auftrag gegebenen Zusammenstellung von Tabellen beschrieben wurde, übernehmen kann und so das ursprünglich gesetzte Ziel erreicht.
Dies ist die Natur der ersten Maschine, die Mr. Babbage erfand. Wir haben gesehen, dass sie beschränkt ist auf solche Fälle, in denen die gewünschten Ergebnisse durch simple Additionen oder Subtraktionen der Ausgangszahlen gewonnen werden können - dass der Automat gleichsam lediglich Ausdruck eines speziellen Theorems der Analysis ist und dass, kurz gesagt, seine Leistungen nicht derart ausgeweitet werden können, dass man damit die unendliche Anzahl von Fragen beantworten könnte, die sich im Gebiet der mathematischen Analysis auftun. Während Mr. Babbage das weite, unbeackerte Feld solcher Fragen betrachtete und dabei die Ansätze seines ersten Aufsatzes ausließ, entwickelte er den Plan eines anderen automatischen Systems, dessen Operationen eine allgemeine algebraische Notation in ihrem Inneren enthalten sollten. Er bezeichnet dieses System in seiner Beschreibung als die Analytische Maschine.
Nachdem der Ausgangspunkt der Problemstellung geklärt wäre, will ich nun die Prinzipien entwickeln, auf denen die Konstruktion seines neueren Automaten beruht. Wenn die Analysis bei der Lösung eines Problems eine Rolle spielt, dann gibt es normalerweise zwei Klassen von Operationen, die ausgeführt werden müssen: erstens die numerischen Berechnungen der verschiedenen Koeffizienten und zweitens deren Verteilungsverhältnis auf die Variable, auf die sie Einfluss nehmen. Wenn wir beispielsweise das Produkt zweier Binome (a+bx) (m+nx) erhalten wollen, dann wird das Produkt umgeformt zu: am + (an + bm) x + bnx2. In diesem Ausdruck errechnen wir zunächst am, an, bm und bn, bilden sodann die Summe an + bm und verteilen zuletzt die berechneten Koeffizienten an die zugehörigen Potenzen der Variablen x. Um diese Operationen mittels eines Automaten zu reproduzieren, muss dieser folglich über zwei grundsätzlich verschiedene Leistungsmerkmale verfügen: er muss erstens numerische Berechnungen ausführen können und die so erhaltenen Werte zweitens korrekt verteilen.
Würden diese beiden Teiloperationen den Eingriff eines Menschen als Betreiber des Automaten notwendig machen, so wäre unter den zwei Aspekten der Korrektheit und des Zeitvorteils jedoch nichts gewonnen. Die Maschine muss als weitere Voraussetzung daher in der Lage sein, selbständig alle aufeinander folgenden Operationen für die Lösung einer ihr gestellten Aufgabe zu erledigen, nachdem zunächst einmalig die numerischen Startbedingungen für ein spezifisches Problem vorgegeben wurden. Daher wird der Automat, nachdem er einmal mit der Art der Berechnung oder dem zu lösenden Problem instruiert wurde, durch die ihm innewohnende Leistungsfähigkeit alle Zwischenschritte selbsttätig ausführen, die zur angestrebten Lösung der Aufgabe führen, dabei jegliche Methoden wie Raten oder Ausprobieren unterlassen und ausschließlich auf direktem Weg die Berechnungen durchführen.
Diese Vorgabe ist notwendig, da die Maschine kein denkendes Wesen, sondern einfach eine Automatik ist, die nach ihr vorgegebenen Gesetzen handelt. Der fundamentale Grundsatz, als Ergebnis der frühesten Forschungen, die der Autor unternehmen musste, war der, dass ein Weg zur Division einer Zahl durch eine andere Zahl gefunden werden musste, der ohne die Methode des Ratens auskam, wie sie in den geläufigen Regeln der Arithmetik angezeigt ist. Die Schwierigkeiten eine solche Methode zu finden waren keineswegs gering zu nennen, doch hing der Erfolg aller weiteren Entwicklung von ihrer Entdeckung ab. Es ist mir unmöglich, hier den Vorgang zu beschreiben, mit dem dieses Ziel erreicht wurde, daher müssen wir uns darauf beschränken anzunehmen, dass die vier Grundrechenarten der Arithmetik - also Addition, Subtraktion, Multiplikation und Division - in direkter Weise im Rahmen der Möglichkeiten einer Maschine ausgeführt werden können. Wenn wir dies voraussetzen, dann ist die Maschine folglich in der Lage, jeden Typus von numerischen Berechnungen auszuführen, der sich auf die eben genannten vier Rechenarten beschränkt. Um nachzuvollziehen, wie die Maschine die Rechenoperationen nach einer vorgegebenen Gesetzmäßigkeit durchführen kann, wollen wir zuerst eine Vorstellung davon vermitteln, wie diese Maschine die Zahlen mit ihren eigenen Mitteln darstellt.
Lassen sie uns nun einen Stapel oder eine senkrechte Spalte mit einer undefinierten Anzahl von runden Scheiben annehmen, die alle auf einer gemeinsamen Achse stecken, um die sie sich frei und einzeln drehen können. Wenn auf den Rand jeder dieser Scheiben die zehn Ziffern des numerischen Alphabets geschrieben sind, dann können wir durch eine Anordnung einer Serie dieser Scheiben aus derselben senkrechten Spalte jede beliebige Zahl darstellen. Es genügt für diesen Zweck, dass die erste Scheibe die Einer repräsentiert, die zweite die Zehner, die dritte die Hunderter und so fort. Nachdem zwei Zahlen in dieser Weise in zwei verschiedene vertikale Spalten eingeschrieben sind, können wir damit beginnen, sie arithmetisch miteinander zu kombinieren und die Ergebnisse in einer dritten Spalte erhalten. Generell könnten wir, wenn wir eine ganze Anzahl von solchen Scheibenstapeln haben, deren Spalten wir mit V0, V1, V2, V3, V4, &c bezeichnen wollen, etwa danach fragen, die Zahl in der Spalte V1 durch die Zahl in der Spalte V4 zu dividieren um das Ergebnis dann aus der Spalte V7 abzulesen. Um eine solche Operation zu bewirken, müssen wir die Maschine in zwei verschiedene Gruppen unterteilten: in der ersten Gruppe würde die Maschine für eine Division vorbereitet und in der zweiten würden sowohl die bei Spalten, auf die sich die Operation bezieht, wie auch die Spalte, in der das Ergebnis erscheinen soll, festgelegt. Wenn nach der Division zum Beispiel eine Addition zweier Zahlen aus zwei anderen Spalten erfolgen soll, dann müssen beide vorherigen Einstellungen gleichzeitig geändert werden. Wenn aber eine Folge von gleichartigen Operationen ausgeführt werden soll, kann die erste Einstellung unverändert bleiben und nur die zweite müsste verändert werden. Die Einstellungen, die den verschiedenen Bereichen der Maschine übermittelt werden müssten, wären also unterteilt in die beiden grundlegenden Klassen:
Erstens, die Klasse der Rechenoperationen.
Zweitens, die Klasse der Variablen.
Die zweite Klasse ist die, welche die Spalten bezeichnet, mit denen die Operation ausgeführt werden soll. Die Rechenoperationen werden von einem speziellen Apparat mit dem Namen Mühle ausgeführt, der selbst wiederum aus einer bestimmten Anzahl Spalten besteht, die denen der Variablen ganz ähnlich sind. Wenn zwei Zahlen miteinander kombiniert werden, startet die Maschine ein Kopie aus den Spalten, in denen die gewünschten Zahlen niedergelegt sind. Dabei erscheint die Null auf jeder Scheibe der zwei vertikalen Spalten, auf denen die Zahlen dargestellt waren und gleichzeitig werden die Ziffern in die Mühle transportiert. Dort arbeitet die Vorrichtung, die für die gewünschte Operation passend eingestellt wurde, diese Rechenoperation ab und überträgt, wenn sie damit fertig ist, das Ergebnis in die zuvor ausgewählte Ergebnisspalte. Die Mühle ist die arbeitende Abteilung der Maschine und die Spalten von Variablen sind der Teil, der zur Einstellung der Startwerte und zur Darstellung der Ergebnisse notwendig ist. Nach den vorangehenden Erklärungen können wir annehmen, dass alle nicht-ganzzahligen und irrationalen Ergebnisse in Form von Dezimalbrüchen dargestellt werden. Wenn wir für jede Spalte 40 Scheiben annehmen, dann ist dieser Umfang ausreichend für jeden im Allgemeinen notwendigen Grad von Näherung.
Nun wenden wir uns der Frage zu, wie die Maschine selbständig und ohne dass ein Mensch Hand anlegen muss, die aufeinander folgenden Einstellungen, die für die Operationen nötig sind, vornehmen kann. Die Lösung dieses Problems wurde von Jacquards Vorrichtung übernommen, die er zur Herstellung von Brokatstoffen in folgender Weise nutzte: —
Man unterscheidet bei gewebten Stoffen normalerweise zwischen zwei Sorten von Fäden: der eine ist der Kettfaden in der Längsrichtung, der andere der Schussfaden oder der rechtwinklige Faden, der von einem Instrument mit der Bezeichnung Schütze durch die vertikalen Kettfäden gekreuzt wird. Wenn ein Brokat-Stoff hergestellt werden soll, müssen bestimmte Fäden jeweils daran gehindert werden, den Schussfaden zu kreuzen. Die geschieht in einer Abfolge, die von der Art des Designs bestimmt ist, das wiedergegeben werden soll. Früher war dieser Prozess langwierig und schwierig und der Arbeiter am Webstuhl musste, indem er sich das zu kopierende Design einprägte, die Bewegungen der einzelnen Fäden selbst vornehmen. Dies bestimmte den hohen Preis dieser Art von Stoffen, speziell solcher Stoffe mit verschiedenfarbigen Fäden. Um die Herstellung zu vereinfachen entwickelte Jacquard einen Plan, wie jede Gruppe von zusammengehörigen Fäden mit einem eigenen Hebel, der jeweils nur für diese eine Gruppe wirkte, bewegt werden konnten. Alle Hebel enden in Stäben, die üblicherweise zu einem Parallelepiped-Bündel mit rechteckiger Grundfläche zusammengefasst werden. Die Stäbe sind zylindrisch und vom jeweiligen Nachbarn durch einen kleinen Abstand getrennt. Der Vorgang des Anhebens von Kettfäden lässt sich so auf die Bewegung der verschiedenen Hebelarme in vorgegebener Anordnung reduzieren. Um dies zu bewirken, nimmt man ein rechteckiges Stück Pappdeckel, das ein wenig größer als die Grundfläche einer Gruppe von solchen Bündeln aus Stäben ist. Wird dieser Pappdeckel an der Abschlussfläche des Bündels angebracht, können sich durch eine Vorwärtsbewegung desselben alle Stäbe eines Bündels gleichzeitig bewegen und somit auch die Kettfäden, die mit jedem Stab verbunden sind. Wenn aber der Pappdeckel nun nicht glatt, sondern an ausgewählten Stellen auf denen Stäbe ruhen, durchlöchert ist, dann können diese Stäbe während der Vorwärtsbewegung der Pappe durch Löcher hindurch gleiten und so an ihren Plätzen verbleiben. Wir sehen, dass es einfach ist, die Position der Löcher in dem Pappdeckel so festzulegen, dass zu jedem gegebenen Moment eine bestimmte Anzahl von Hebeln und folglich Gruppen von Kettfäden angehoben sind, während der Rest unverändert bleibt. Wenn dieser Prozess schrittweise mit den Regeln für ein auszuführendes Muster wiederholt wird, verstehen wir, wie dies ein Muster auf dem Stoff ergibt. Zu diesem Zweck benötigen wir lediglich eine Zusammenstellung von Pappkarten, die nach der Abfolgeregel des Musters eine nach der anderen angeordnet sind. Führt man diese verbundenen Pappkarten nun über einen eckigen Holm, der so mit dem Webstuhl verbunden ist, dass er bei jedem Schuss des Schützen eine neue Karte vorlegt, die anschließend gleichmäßig gegen das Bündel von Hebelarmen gedrückt wird, so wird die Aufgabe des Anhebens der Kettfäden regelmäßig ausgeführt. Nun sehen wir, wie Brokat-Stoffe mit einer Präzision und Geschwindigkeit hergestellt werden können, die zuvor schwer erreichbar war.
Anordnungen ähnlich wie die eben beschriebene wurden auch bei der Analytischen Maschine angewandt. Sie enthält zwei prinzipiell verschiedene Typen von Karten: erstens Operations-Karten, durch die Teile der Maschine so eingestellt werden, dass sie eine bestimmte Abfolge von Rechenoperationen festlegen, wie Additionen, Subtraktionen, Multiplikationen und Divisionen; zweitens Variablen-Karten, die bestimmen in welche Spalten die Eingaben und Ergebnisse darzustellen sind. Während der Bewegung dieser Karten stellen sie verschiedene Teile der Maschine entsprechend der Art des Vorgangs ein, den sie bewirken sollen und die Maschine führt zur selben Zeit diese Vorgänge mit den verschiedenen Teilen, die ihren Mechanismus ausmachen, aus.
Um diese Sache besser zu verstehen, wollen wir als Beispiel die Lösung von zwei Gleichungen ersten Grades mit zwei Unbekannten wählen. In den folgenden beiden Gleichungen seien x und y die unbekannten Größen: —
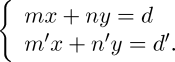
Wir leiten daraus ab ![]() und für y die entsprechende Gleichung. Weiterhin sollen V0, V1, V2, &c. die verschiedenen Spalten bezeichnen, welche die Zahlenwerte enthalten. Lassen sie uns annehmen, dass die ersten acht Spalten ausgewählt wurden, um folgende Zahlen zu repräsentieren: m, n, d, m', n', d', n und n', mit V0=m, V1=n, V2=d,
V3=m', V4=n', V5=d', V6=n,
V7=n'.
und für y die entsprechende Gleichung. Weiterhin sollen V0, V1, V2, &c. die verschiedenen Spalten bezeichnen, welche die Zahlenwerte enthalten. Lassen sie uns annehmen, dass die ersten acht Spalten ausgewählt wurden, um folgende Zahlen zu repräsentieren: m, n, d, m', n', d', n und n', mit V0=m, V1=n, V2=d,
V3=m', V4=n', V5=d', V6=n,
V7=n'.
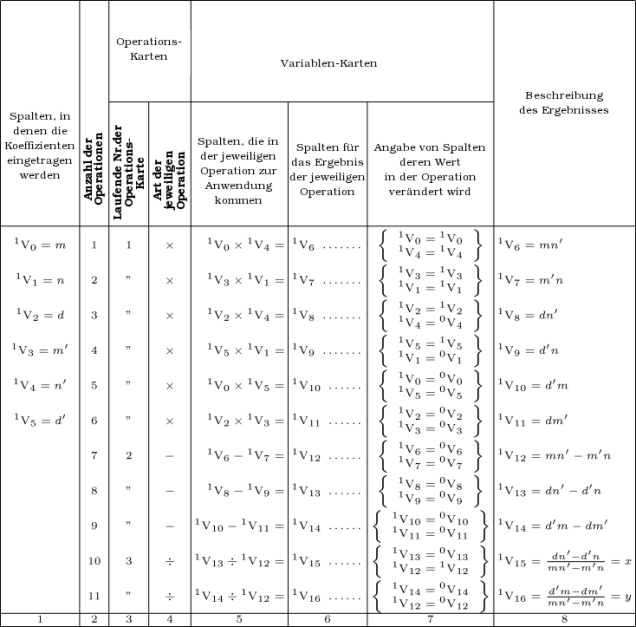
Die Abfolge von Operationen, die durch die Karten bestimmt werden, sowie die Ergebnisse der Operationen, können in folgender Tabelle dargestellt werden: —
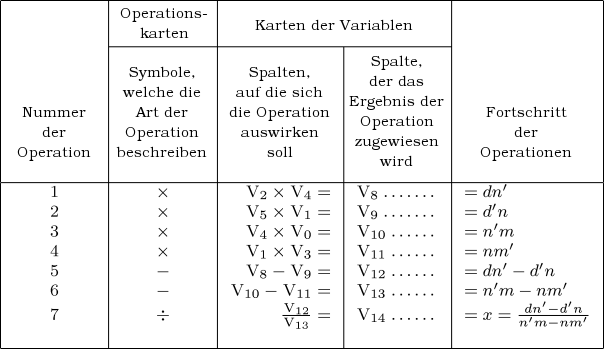
Da die Karten nichts weiter machen, als die Art und Weise zu beschreiben, in der die Maschine festgelegte Spalten bearbeitet, wird klar, dass wir die numerischen Werte für jeden speziellen Fall einstellen müssen. Im ausgewählten Beispiel müssen wir die Zahlenwerte von m, n, d, m', n', d' in der Reihenfolge der bezeichneten Spaltennummern einstellen und die Maschine wird nach Inbetriebnahme den Wert der Unbekannten x für diesen speziellen Fall ergeben. Um den Wert für y zu erhalten, ist eine weitere Folge von Operationen notwendig, die ganz ähnlich den vorangegangenen ablaufen muss. Aber wir sehen, dass nur vier weitere Operationen notwendig sind, da der Nenner des Ausdrucks für y, abgesehen vom Vorzeichen, derselbe ist wie der für x, nämlich n'm-nm'. In der obigen Tabelle sind in der Spalte für die Operationen vier aufeinander folgende Multiplikationen ausgewiesen, danach zwei Subtraktionen und schließlich eine Division. Daher benötigen wir, wenn wir es so wollen, lediglich drei Operations-Karten. Um dies zu erreichen genügt es, in die Maschine eine Vorrichtung einzuführen, die zum Beispiel nach der ersten Operation die Karte, die diese Operation bezeichnet, so lange nicht durch die nächste Karte ersetzt, bis dieselbe Operation vier Mal wiederholt wurde. Im vorangegangenen Beispiel haben wir gesehen, dass wir, um den Wert von x zu finden, die Koeffizienten m, n, d, m', n' und d' in insgesamt acht Spalten eintragen mussten und dabei n und n' zweimal einzugeben hatten. Wenn wir y nach derselben Methode berechnen wollten, würde die Berechnung zwölf verschiedene Spalten für die Koeffizienten benötigen. Dieser Prozess lässt sich aber vereinfachen und es lässt sich so die Wahrscheinlichkeit verringern, dass bei der wiederholten Eingabe von denselben Werten in verschiedene Spalten, noch vor dem Start der Maschine, Fehler gemacht werden. Um diese Vereinfachung zu verstehen, müssen wir uns erinnern, dass jede Zahl, die in eine Spalte eingetragen wurde, vor der arithmetischen Kombination mit einer anderen Zahl aus ihrer eigenen Spalte in die Mühle kopiert werden muss. Im diskutierten Beispiel nähmen wir die beiden Koeffizienten m und n', die beide in jeweils zwei verschiedenen Produkten vorkommen, nämlich m in mn' sowie md' und n' in mn' sowie n'd. Diese Koeffizienten werden in den Spalten V0 und V4 voreingestellt. Wenn wir die Serie der Operationen mit dem Produkt von m mal n' beginnen lassen, werden diese beiden Zahlen aus ihren Spalten V0 und V4 in die Mühle übertragen, die sie dann multiplizieren und die das Ergebnis danach in eine Spalte, zum Beispiel in V6, ausgeben wird. Da diese beiden Zahlen in einer weiteren Operation noch einmal verwandt werden, könnte die Mühle, während sie das Produkt berechnet, sie gleichzeitig wiederum in zwei beliebige Spalten kopieren, die von den Karten festgelegt werden. Im aktuellen Fall gibt es keinen Grund, warum die Zahlen nicht in ihren ursprünglichen Spalten erscheinen sollten. Wir nehmen also an, dass sie wiederum in V0 und V4 erscheinen. Kurz gesagt würden sie nicht am Ende der Operation verschwinden ohne wieder aufzutauchen, bis sie für alle Kombinationen, die sie benötigten, zur Verfügung standen.
Wir sehen nun, wie die komplette Zusammenstellung der benötigten Operationen für die zuvor bezeichneten beiden Gleichungen ersten Grades vollständig mit der folgenden Tabelle beschrieben werden könnte: —
|
|
Durch einen Klick auf die Tabelle erhalten Sie eine größere Darstellung. Der „Zurück”-Button ihres Browser bringt Sie anschließend wieder zu diesem Dokument. |
Um die Wahrscheinlichkeit von Falscheingaben der numerischen Daten eines Problems zu minimieren, werden diese nacheinander in eine der Spalten der Mühle übertragen. Diese Daten werden dann nacheinander mittels für diesen Zweck vorgesehener Karten auf die gewünschten Spalten platziert, ohne dass der Betreiber diesem Vorgang Beachtung widmen müsste. Der Mensch kann sich mit ungeteilter Aufmerksamkeit einfach der Eingabe dieser Zahlen widmen.
Im Anschluss an diese Beschreibung erkennen wir, dass sich die Zusammenstellung der Spalten mit Variablen wie ein Zahlenspeicher darstellt, der von der Mühle aufgefüllt wird und der mittels Karten der Maschine vorgegebenen Regeln, diese Zahlen abwechselnd vom Speicher in die Mühle und von der Mühle in den Speicher überträgt, während sie gleichzeitig Umwandlungen entsprechend der Art der vorgesehenen Berechnungen unterliegen.
Bis dato wurden mögliche Vorzeichen der Ergebnisse nicht erwähnt und die Maschine wäre bei weitem nicht perfekt, wenn sie nicht in der Lage wäre, positive wie negative Zahlen miteinander zu kombinieren und darzustellen. Um dieses Ziel zu erreichen gibt es über jeder Spalte, sowohl in der Mühle, wie auch im Speicher, eine den anderen Scheiben einer Spalte ganz ähnliche Scheibe. Je nachdem, ob die Ziffer dieser Scheibe gerade oder ungerade ist, wird die in dieser Spalte eingetragene Zahl entweder als positive oder negative Zahl betrachtet. Mit diesem Vorwissen können wir nachvollziehen, wie die Vorzeichen in der Maschine algebraisch kombiniert werden. Wenn eine Zahl aus dem Speicher in die Mühle übertragen werden soll oder vice versâ, wird sie, in der zuvor beschriebenen Weise durch Karten bestimmt, immer zusammen mit ihrem Vorzeichen kopiert. Nun werden zwei beliebige Zahlen, auf die wir nun eine arithmetische Operation anwenden wollen, zusammen mit ihren jeweiligen Vorzeichen in der Mühle platziert. Nehmen wir an, wir wollten sie zunächst addieren, das heißt die Operations-Karten legen eine Addition fest: wenn beide Zahlen dasselbe Vorzeichen haben, so wird eine der beiden Zahlen vollständig von dort kopiert, wo sie eingeschrieben war und wird sich zu der Spalte, die die zweite Zahl enthält, hinzu addieren. Die Maschine wird während dieser Operation mit Hilfe einer bestimmten Vorrichtung in der Lage sein, jegliche Bewegung der Scheibe für das Vorzeichen in der Spalte, in der die Addition ausgeführt wird, zu verhindern und daher wird das Ergebnis dasselbe Vorzeichen wie die beiden vorgegebenen Zahlen anzeigen. Falls die beiden Zahlen verschiedene Vorzeichen haben, wird die von der Operations-Karte bestimmte Addition durch den Eingriff einer Vorrichtung, die von den unterschiedlichen Vorzeichen aktiviert wird, in eine Subtraktion umgewandelt. Da eine Subtraktion nur von der größeren der beiden Zahlen möglich ist, muss dafür Sorge getragen werden, dass die Scheibe mit dem Vorzeichen der größeren Zahl sich nicht bewegen kann, während die kleinere der beiden Zahlen aus ihrer Spalte kopiert und von der anderen subtrahiert wird, sodass als Vorzeichen das der größeren Zahl erhalten bleibt, wie es in der Tat sein muss. Die Vorzeichen-Kombinationen, die bei der algebraischen Subtraktion auftreten, sind entsprechend des zuvor beschriebenen. Lassen sie uns weiter gehen zur Multiplikation. Wenn zwei Zahlen gleichen Vorzeichens miteinander multipliziert werden, dann ist das Resultat ebenfalls positiv. Unterscheiden sich die beiden Vorzeichen, dann muss das Produkt negativ sein. Damit die Maschine diese Gesetzmäßigkeit einfach umsetzen kann, betrachten wir lediglich die Spalte, in der das Produkt der beiden Zahlen erscheint: die Ziffer, welche das Vorzeichen des Ergebnisses anzeigt, wird durch eine Addition der Vorzeichen-Ziffern der beiden ausgewählten Zahlen bestimmt. Es ist offensichtlich, dass wenn die Ziffern der Vorzeichen beide gerade oder beide ungerade waren, ihre Summe eine gerade Ziffer ist und somit eine positive Zahl bezeichnet. Wenn aber von den Ziffern der Vorzeichen die eine gerade und die andere ungerade ist, dann wird auch ihre Summe eine ungerade Ziffer sein und somit eine negative Zahl anzeigen. Im Falle der Division müssen die Ziffern der Scheiben voneinander subtrahiert, statt zueinander addiert werden, was zu Ergebnissen analog des zuvor Beschriebenen führt. Wenn also die Ziffern beide gerade oder beide ungerade sind, ist das Ergebnis der Subtraktion gerade, andernfalls wird es ungerade sein. Wenn ich hier entweder von der Addition oder der Subtraktion der Ziffern spreche, welche die Vorzeichen repräsentieren, dann meine ich damit lediglich, dass sich die eine der Vorzeichen-Scheiben um die Anzahl von Positionen, die von der Ziffer der anderen Vorzeichen-Scheibe dargestellt werden, entweder vorwärts oder rückwärts bewegt. Die vorangehende Erklärung zeigt uns, dass es möglich ist, die Vorzeichen von zwei Größen mechanisch so zu kombinieren, dass wir die in der Algebra festgelegten Ergebnisse erhalten.
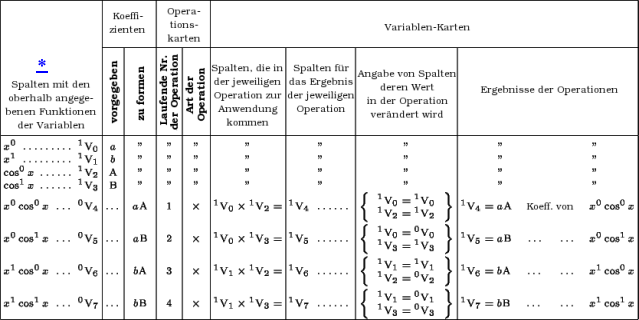
Die Maschine ist nicht nur in der Lage, die Art numerischer Berechnungen durchzuführen, die auf einer gegebenen algebraischen Gleichung beruhen. Sie ist vielmehr auch für analytische Berechnungen mit einer oder mehreren Variablen geeignet. Wir müssen davon ausgehen, dass die zu bearbeitende analytische Gleichung in eine Potenzgleichung der Variablen umgeformt werden kann oder in eine Gleichung bestimmter Funktionen derselben Variablen, wie etwa der Kreisfunktionen. Gleiches gilt für das gewünschte Ergebnis. Wenn wir annehmen, die jeweiligen Potenzen einer Variablen seien oberhalb der Spalten des Speichers in einer Weise notiert, wie sie sich aus den vorgegebenen Regeln der umgeformten Gleichung ergeben, dann können die Koeffizienten der verschiedenen Terme jeweils in der zugehörigen Spalte darunter platziert werden. Auf diese Art erhalten wir die Darstellung einer analytischen Entwicklung und indem wir einige der sie bildenden Terme als unveränderlich ansehen, wird die Problemstellung darauf reduziert, ihre Koeffizienten entsprechend der Gesetzmäßigkeiten in der Art der Frage zu errechnen. Um diesen Sachverhalt klarer darzustellen, nehmen wir folgendes sehr einfache Beispiel an, in dem wir (a + bx¹) mit (A + B cos¹ x) multiplizieren wollen. Wir beginnen damit, die Funktionen x0, x¹, cos0 x und cos¹ x über den Spalten V0, V1, V2 und V3 einzutragen. Aus der Form der beiden zu kombinierenden Funktionen ergibt sich die Art der folgenden, ihre Produkte ausmachenden Terme: x0·cos0 x, x0·cos¹ x, x¹·cos0 x und x¹·cos¹ x, die wir oberhalb der Spalten V4, V5, V6 und V7 eintragen. Die vorgegebenen Koeffizienten für x0, x¹, cos0 x und cos¹ x werden mit Hilfe der Mühle in die Spalten V0, V1, V2 sowie V3 übertragen. Damit sind die einfachen Daten des Problems eingestellt. Die Aufgabe der Maschine ist es nun, die Lösungen des Problems zu erarbeiten, also die Koeffizienten zu finden, die in den Spalten V4, V5, V6 und V7 erscheinen müssen. Um dies zu erreichen, geben wir die nach den bekannten Regeln zur Bildung dieser Koeffizienten erstellten Karten in folgender Tabelle an: —
|
|
Durch einen Klick auf die Tabelle erhalten Sie eine größere Darstellung. Der „Zurück”-Button ihres Browser bringt Sie anschließend wieder zu diesem Dokument. Fußnote im Diagramm lesen. |
Nun wird verständlich, wie das Prinzip der zuvor beschriebenen Entwicklung ganz allgemein für jede Art von Vorgang angewandt werden kann, der sich als eine Abfolge solcher Berechnungen darstellen lässt. Es genügt, dass die Gesetzmäßigkeiten zur Bildung der Koeffizienten bekannt sind und dass diese Gesetzmäßigkeiten mittels Karten der Maschine eingegeben werden, welche sodann alle notwendigen Berechnungen selbständig durchführen und das gesuchte Ergebnis errechnen wird. Wenn beispielsweise eine periodische Folge vorliegt, deren Koeffizienten alle gleichförmig aufgebaut sind, dann können die Operationen für einen der Koeffizienten für alle anderen wiederholt werden. Es wird lediglich eine Veränderung in den von der Operation betroffenen Stellen geben. Anders gesagt werden die Operationen mit wechselnden Spalten ausgeführt. Da ganz allgemein jeder analytische Ausdruck dazu geeignet ist, durch eine geordnete Serie von bestimmten Funktionen der Variablen dargestellt zu werden, verstehen wir auch, warum die Maschine zu all den analytischen Berechnungen fähig ist, deren Gleichungen zu einer durch bestimmte Gesetzmäßigkeiten vorgegebenen Anordnung und Verteilung von Koeffizienten auf die Variablen umgeformt werden können.
Wir können aus diesen Erklärungen nun die folgende wichtige Konsequenz herleiten, dass diese Karten, die lediglich die Natur der auszuführenden Operationen und die Spalten der in der Berechnung zu nutzenden Variablen beschreiben, in sich selbst die generelle Anwendbarkeit der Analysis bergen, für die sie in der Tat nichts weiter als eine Übersetzung darstellen. Wir wollen nun weiterhin einige der Schwierigkeiten untersuchen, welche die Maschine auflösen muss, falls sie den komplette Bereich der Analysis umfassen soll. Es existieren bestimmte Funktionen, die im Nulldurchgang oder im Unendlichen ihre Natur verändern oder deren Werte für den Durchgang durch diese Grenzen nicht angebbar sind. Wenn solche Fälle eintreten, kann die Maschine mit Hilfe einer Glocke ein Signal geben, dass ein solcher Durchgang durch Null oder Unendlich stattfindet und anhalten, bis der Betreiber eine andere Aufgabe eingestellt hat und sie wieder in Betrieb setzt. Wenn dieser Prozess vorauszusehen war, kann die Maschine statt zu läuten sich auch selbst so neu einstellen, dass eine neue Folge von Karten für den Fall vorgelegt wird, dass ein Durchgang durch Null oder Unendlich erfolgt. Diese neuen Karten können den vorherigen direkt folgen, werden aber nur dann ins Spiel gebracht, falls der eine oder der andere der beiden vorgenannten Fälle eintritt.
Lassen Sie uns einen Term der Form abn annehmen. Da die Karten nichts als eine Übersetzung der analytischen Formel darstellen, muss ihre Anzahl in diesem speziellen Fall für jeden beliebigen Wert von n gleich bleiben (wir nehmen für den Moment an, dass n eine ganze Zahl ist). Anders gesagt ist n die Anzahl der Multiplikationen, die notwendig ist, um b zur n. Potenz zu erheben. Der Exponent n bezeichnet also, dass b genau n mal mit sich selbst multipliziert werden muss und da all diese Operationen von der gleichen Art sind genügt es, eine einzelne Operations-Karte dafür einzusetzen, welche die Multiplikation festlegt.
Wenn aber n in diesem speziellen Fall berechnet werden soll, muss die Maschine als weitere Einschränkung die Anzahl der Multiplikationen entsprechend der vorgegebenen Werte begrenzen. Der Vorgang könnte in folgender Weise angelegt werden. Die drei Zahlen a, b und n werden in drei verschiedene Spalten des Speichers eingetragen, die wir mit V0, V1, V2 bezeichnen wollen. Das Ergebnis abn selbst soll in der Spalte V3 erscheinen. Nachdem die Zahl n der Maschine eingegeben wurde, wird eine Karte eine spezielle Register-Vorrichtung veranlassen, (n-1) anzuzeigen und zur selben Zeit die Multiplikation von b mal b ausführen. Wenn diese Multiplikation beendet ist, wird die Register-Vorrichtung eine Einheit subtrahiert haben und nun nur noch (n-2) anzeigen, während die Maschine wiederum die Zahl b aus der Spalte V1 mit dem Produkt b2 in der Spalte V3 multiplizieren wird, was sodann b3 ergibt. Eine weitere Einheit wird von Register-Vorrichtung subtrahiert und derselbe Prozess wird fortwährend wiederholt, bis die Anzeige Null erreicht ist. Es wird folglich die Zahl bn in der Spalte V3 eingetragen sein, wenn die Maschine im weiteren Ablauf der Operationen das Produkt von bn und a anfordert. Die gewünschte Berechnung wird also ausgeführt, ohne dass die Anzahl der Operations-Karten abhängig vom Wert von n variiert werden muss. Wenn n negativ wäre, würden die Karten statt der Multiplikation von a mit bn die Division von a durch bn anfordern. Wir können dies leicht nachvollziehen, da jede Zahl mit ihrem zugehörigen Vorzeichen eingetragen ist und folglich Einfluss auf die Art der auszuführenden Operation nehmen kann. Schließlich ist für den Fall, dass n ein Bruch der Form p/q ist, eine weitere Spalte für die Eintragung des Wertes von q notwendig und die Maschine würde zwei Gruppen von Abläufen ausführen: den ersten, um b zur Potenz p zu erheben und den zweiten, um die q. Wurzel aus der so erhaltenen Zahl zu ziehen.
In einem weiteren Beispiel könnte es notwendig werden, einen Ausdruck der Form ax m+bx n mit einem zweiten der Form Ax p+Bx q zu multiplizieren und das Produkt auf die kleinste Anzahl von Termen mit gleichen Indizes zu reduzieren. Wenn beide Faktoren nach x sortiert werden, dann wäre das in allgemeiner Form dargestellte Ergebnis der Multiplikation gleich Aax m+p+Abx n+p+Bax m+q+Bbx n+q. Bis zu diesem Punkt liegt in dem Vorgehen keine besondere Schwierigkeit, aber nehmen wir nun einmal an, dass wir m=p und n=q haben und dass wir die beiden mittleren Terme zu einem einzigen (Ab+Ba)x m+q zusammenziehen wollen. Für diesen Zweck könnten die Karten angeben, dass m+q und n+p in die Mühle übertragen und dort voneinander subtrahiert werden sollen. Wenn kein Rest bleibt, wie im Falle der aktuellen Annahme, dann wird die Mühle durch die nächsten Karten aufgefordert, die beiden Koeffizienten Ab und Ba zu addieren und sie in diesem Stadium als Koeffizienten für den einzigen Term x n+p=x m+q zu verwenden.
Dieses Beispiel legt nahe, wie die Karten all die Operationen wiedergeben können, die auch ein Intellekt ausführt, um ein bestimmtes Ergebnis zu erreichen, wenn nur die Operationen selbst präzise genug definiert werden können.
Lassen Sie uns nun den folgenden Ausdruck untersuchen: —
der, wie wir wissen, gleich dem Verhältnis des Umfangs zum Durchmesser eines Kreises wird, wenn n unendlich wird. Wir können die Maschine auffordern, nicht nur die Berechnung dieser Bruchdarstellung durchzuführen, sondern auch anzuzeigen, wann der Wert gleich dem Verhältnis von Umfang zu Durchmesser wird, also dem nicht berechenbaren Fall, wenn n gegen Unendlich geht. Beachten Sie hierbei, dass wir die Maschine somit auffordern, ein ihr selbst unbekanntes und unzugängliches Ergebnis zu interpretieren, da sie ja kein denkendes Wesen ist. Trotzdem könnte, wenn wir den Kosinus von n=1/0 vorhergesehen haben, eine Karte die Einsetzung des bekannten Wertes von ![]() (
(![]() ist das Verhältnis von Umfang zu Durchmesser) festlegen, ohne dass die unendliche Abfolge von Berechnungen ausgeführt würde. Dies zu erreichen würde lediglich voraussetzen, dass die Maschine eine spezielle Karte enthalten kann, deren Aufgabe es ist die Zahl
ist das Verhältnis von Umfang zu Durchmesser) festlegen, ohne dass die unendliche Abfolge von Berechnungen ausgeführt würde. Dies zu erreichen würde lediglich voraussetzen, dass die Maschine eine spezielle Karte enthalten kann, deren Aufgabe es ist die Zahl ![]() in direkter und unabhängiger Weise in einer Spalte zu platzieren, die auf der Karte angegeben ist. An dieser Stelle wollen wir nun eine dritte Art von Karten einführen, die wir Zahlen-Karten nennen können. Es gibt bestimmte Zahlen, so wie jene, die das Verhältnis von Umfang zu Durchmesser beschreibt, wie die Bernoulli-Zahlen &c., die häufiger in Berechnungen vorkommen werden. Um die Notwendigkeit einer bei jeder Verwendung neuerlichen Berechnung dieser Zahlen zu vermeiden, können bestimmte Karten kombiniert werden, die solche vorgefertigten Zahlen in die Mühle eingeben, von wo sie hernach in den für sie bestimmten Spalten des Speichers platziert werden. Durch diese Möglichkeit wird die Maschine zugänglich für Vereinfachungen in der Art einer Anwendung von numerischen Tabellen. Genauso wäre es mit Hilfe dieser Karten möglich, die Logarithmen von Zahlen einzuführen, aber vielleicht wäre das im Falle der Logarithmen nicht die kürzeste oder passendste Methode, da die Maschine in der Lage sein könnte, die Berechnungen in viel rascheren Kombinationen auszuführen, die sie auf Grund ihrer Geschwindigkeit bei der Ausführung der vier Grundrechenarten erreicht. Um einen Eindruck von dieser Geschwindigkeit zu vermitteln, müssen wir nur erwähnen, dass Mr. Babbage angibt mit seiner Maschine innerhalb von drei Minuten die Multiplikation zweier Zahlen mit je zwanzig Ziffern ausführen zu können.
in direkter und unabhängiger Weise in einer Spalte zu platzieren, die auf der Karte angegeben ist. An dieser Stelle wollen wir nun eine dritte Art von Karten einführen, die wir Zahlen-Karten nennen können. Es gibt bestimmte Zahlen, so wie jene, die das Verhältnis von Umfang zu Durchmesser beschreibt, wie die Bernoulli-Zahlen &c., die häufiger in Berechnungen vorkommen werden. Um die Notwendigkeit einer bei jeder Verwendung neuerlichen Berechnung dieser Zahlen zu vermeiden, können bestimmte Karten kombiniert werden, die solche vorgefertigten Zahlen in die Mühle eingeben, von wo sie hernach in den für sie bestimmten Spalten des Speichers platziert werden. Durch diese Möglichkeit wird die Maschine zugänglich für Vereinfachungen in der Art einer Anwendung von numerischen Tabellen. Genauso wäre es mit Hilfe dieser Karten möglich, die Logarithmen von Zahlen einzuführen, aber vielleicht wäre das im Falle der Logarithmen nicht die kürzeste oder passendste Methode, da die Maschine in der Lage sein könnte, die Berechnungen in viel rascheren Kombinationen auszuführen, die sie auf Grund ihrer Geschwindigkeit bei der Ausführung der vier Grundrechenarten erreicht. Um einen Eindruck von dieser Geschwindigkeit zu vermitteln, müssen wir nur erwähnen, dass Mr. Babbage angibt mit seiner Maschine innerhalb von drei Minuten die Multiplikation zweier Zahlen mit je zwanzig Ziffern ausführen zu können.
Vielleicht erscheint Ihnen die für die Berechnung einiger eher komplizierter Probleme notwendig werdende immense Anzahl von Karten als eine Hürde, aber dieser Schein trügt. Es gibt keine Grenze für die Anzahl an Karten, die eingesetzt werden können. Bestimmte Stoffe benötigen für ihre Herstellung mehr als zwanzigtausend Karten und wir können selbst diese Menge fraglos noch weit überschreiten.
In einer Zusammenfassung dessen, was wir über die Funktion der Analytischen Maschine erläuterten, können wir nun abschließend sagen, dass sie auf zwei Prinzipien basiert: erstens auf dem Faktum, dass jede arithmetische Berechnung im Endeffekt auf den vier Grundrechenarten — Addition, Subtraktion, Multiplikation und Division — beruht, sowie auf der zweitens bestehenden Möglichkeit, jede analytische Berechnung in eine zur Ermittlung der Koeffizienten für mehrere Terme einer bestimmten Folge notwendige Rechnung um zu formen. Wenn dieses zweite Prinzip gilt, dann liegen alle Operationen der Analysis innerhalb der Fähigkeiten der Maschine. Aus einem anderen Blickwinkel gesehen ermöglichen die Karten eine so allgemeine Anwendbarkeit der Maschine, die der von algebraischen Formeln entspricht, da solche Formeln schlicht die Art und Anordnung der Operationen vorgeben, die zum Erreichen eines bestimmten Ergebnisses notwendig sind und da die Karten der Maschine lediglich genau solche Operationen vorgeben. Einzig die numerischen Daten eines konkreten Problems müssen im Einzelfall eingegeben werden, damit die Mechanismen für jede beliebige Aufgabe danach in Aktion treten können. Daher kann man dieselbe Folge von Karten für all die Fragen, deren gleichartige Natur nichts weiter als geänderte numerische Daten erfordert, wiederholt einsetzen. In diesem Lichte betrachtet stellen die Karten nicht mehr als eine Übersetzung der algebraischen Formeln dar oder, um es besser zu formulieren, eine neue Form der analytischen Notation.
Da die Maschine eine Betriebsart hat, in der sie in besonderer Weise auf sich selbst reagiert, wird es in jedem Einzelfall notwendig sein, die Abfolge der Berechnungen so anzuordnen, dass sie sich an den Fähigkeiten der Maschine orientiert. Dieser oder jener Prozess mag für einen menschlichen Rechner zwar sehr leicht, für die Maschine aber langwierig und kompliziert sein oder auch vice versâ.
Da in allgemeinster Betrachtungsweise die wesentliche Aufgabe der Maschine darin liegt, vorgegebenen Gesetzen folgende Berechnungen von numerischen Koeffizienten durchzuführen und diese dann auf die passenden Spalten der Variablen zu verteilen, folgt daraus, dass die Interpretation der Formeln und der Ergebnisse jenseits ihrer Möglichkeiten liegt, es sei denn, dass eine solche Interpretation selbst vermittels Gleichungen in den von der Maschine angewandten Symbolen möglich wäre. So ist die Maschine zwar nicht ein denkendes Wesen, aber doch ein Wesen, das intelligente Konzept durchführen kann. Die Karten sind Ausdruck dieser Konzepte und übertragen die zur Umsetzung notwendigen Aufträge an die verschiedenen Verkettungen von Mechanismen, die diese Maschine ausmachen. Wenn diese Maschine einmal konstruiert sein wird, besteht die verbleibende Schwierigkeit darin, die notwendigen Karten zu erstellen. Da diese aber lediglich Übersetzungen von algebraischen Formeln sind, wird es durch eine einfache Notation möglich sein, diese Aufgabe einem Arbeiter zu übertragen. Die gesamte intellektuelle Arbeit wird sich auf die Vorbereitung der Formeln beschränken, die für eine Berechnung durch die Maschine angepasst werden müssen.
Wenn wir nun zugeben, dass eine solche Maschine konstruiert werden kann, dann können wir fragen: Wozu wird sie dienen? Wir rekapitulieren noch einmal die Vorzüge. Erstens: perfekte Korrektheit. Wir wissen, dass numerische Berechnungen generell den Stolperstein bei der Lösung von Problemen darstellen, da sich leicht Fehler einschleichen und es bei weitem nicht immer leicht ist, diese Fehler hernach aufzudecken. Die Maschine aber bietet durch ihre besondere Natur des Abarbeitens von Operationen, ohne die Notwendigkeit von menschlichem Eingreifen, jede Voraussetzung für Korrektheit. Zusätzlich enthält sie eine eigene Überprüfung, da sie am Ende jeder Operation nicht nur die Ergebnisse, sondern ebenso die numerischen Daten der Fragestellung ausgibt, was eine Überprüfung der Korrektheit der gestellten Frage einfach macht. Zweitens: die Zeitersparnis. Um uns selbst davon zu überzeugen, brauchen wir uns nur zu erinnern, dass die Multiplikation zweier Zahlen, bestehend aus je zwanzig Ziffern, längstens drei Minuten benötigt. Weiterhin kann die Maschine, wenn sie eine längere Folge von identischen Berechnungen ausführen soll, wie sie für die Erstellung von numerischen Tabellen benötigt wird, dazu gebracht werden, mehrere Ergebnisse zur selben Zeit zu liefern, was die Anzahl der Vorgänge insgesamt deutlich verkürzen wird. Drittens: Intelligenz-Optimierung. Schon für eine einfache arithmetische Berechnung muss die durchführende Person einige Fähigkeiten besitzen und wenn wir zu komplizierteren Berechnungen übergehen und algebraische Formeln in speziellen Fällen nutzen wollen, setzt dies mathematische Studien zur Aneignung von Wissen in bestimmtem Umfang voraus. Die Maschine aber, mit ihrer Fähigkeit all diese rein mechanischen Operationen durchzuführen, erspart diese intellektuelle Arbeit, die daher profitabler eingesetzt werden kann. Die Maschine kann als eine regelrechte Ziffernfabrik angesehen werden, die ihre Hilfe den vielen nützlichen Wissenschaften und Künsten offeriert, welche von Zahlen abhängig sind. Wer aber kann die Konsequenzen einer solchen Erfindung wirklich voraussehen? In Wahrheit mag es viele wunderbare Beobachtungen für den Fortschritt der Wissenschaften geben, die wegen der fehlenden Leistung zur Berechnung von Ergebnissen praktisch blockiert sind! Und bedenken wir, welche Entmutigung die Aussicht auf eine langwierige und trockene Berechnung für einen genialen Geist bedeutet, der seine Zeit ausschließlich mit Nachdenken verbringen will und sie stattdessen von der Notwendigkeit zu routinemäßigen Operationen gestohlen sieht! Doch nur durch den arbeitsreichen Weg der Analysis kann er die Wahrheit finden. Er kann sie nur durch die Führung der Zahlen verfolgen, weil wir ohne die Zahlen den Schleier, der die Mysterien der Natur verdeckt, nicht lüften können. Die Realisierung der Idee der Konstruktion einer solchen Apparatur, welche menschliche Schwächen in diesem Forschungsbereich ausgleicht, würde eine glorreiche Epoche in der Geschichte der Wissenschaften einläuten. Die Pläne für all die verschiedenen Teile und für all die Räderwerke, die diese immense Apparatur ausmachen, sind ausgearbeitet und ihre Abläufe sind untersucht, aber sie sind noch nicht vollständig in den Zeichnungen und in der mechanischen Beschreibung zusammengefasst. Die Zuversicht, welche die Genialität von Mr. Babbage auslösen muss, bietet hinreichend Grund für die Hoffnung, dass diese Unternehmung von Erfolg gekrönt sein wird und sie bietet Anlass dafür, die Sehnsucht nach der Umsetzung dieses Projektes zu nähren, während wir der sie ausführenden Intelligenz unsere Huldigung versichern.

|
| Ada Augusta, Herzogin von Lovelace |
Die spezielle Funktion, deren Integral zu errechnen die Differenzmaschine konstruiert wurde, ist:
Der Zweck, für den die Maschine ausdrücklich erdacht und den zu erreichen sie angepasst wurde, war die Berechnung von nautischen und astronomischen Tabellen. Das Integral von
| ist | uz = a+bx+cx2+dx3+ex4+fx5+gx6, |
wobei die Konstanten a, b, c, &c. auf den sieben Spalten der Scheiben, aus denen die Maschine besteht, eingestellt werden. Die Maschine kann daher akkurat und unbegrenzt alle Reihen berechnen, deren genereller Term in der obigen Formel enthalten ist. Sie kann ferner näherungsweise zwischen größeren oder kleineren Intervallen bei solchen Reihen tabellieren, die der Methode der Differenzen zugänglich sind.
Im Gegensatz dazu ist die Analytische Maschine nicht bloß für das Tabellieren der Ergebnisse einer einzigen, speziellen Funktion ausgelegt, sondern vielmehr für die Entwicklung und Tabellierung beliebiger Funktionen. Die Maschine könnte tatsächlich als die manifestierte Umsetzung einer beliebigen Funktion jedweden Grades von Generalität und Komplexität beschrieben werden, so wie zum Beispiel
was, wie wir sehen werden, eine Funktion aller möglichen anderen Funktionen von beliebigen Größen ist.
In einem bestimmten Zustand der Maschine, den wir den neutralen oder den Null-Zustand nennen können, ist sie bereit, durch die Vorgabe von Karten, die einen Teil ihres Mechanismus ausmachen (und die dem Prinzip der Karten des Jacquard-Webstuhls entsprechen), die speziellen Funktionen, die wir entwickeln oder tabellieren wollen, entgegen zu nehmen. Diese Karten enthalten (in einer Weise, die im Memorandum selbst erklärt ist) die Gesetzmäßigkeiten zur Entwicklung einer bestimmten Funktion, die untersucht werden kann und sie veranlassen den Mechanismus dazu, in einer bestimmten, korrespondierenden Reihenfolge zu agieren. Einer der einfachsten Fälle wäre zum Beispiel anzunehmen, dass
die spezielle Funktion sei:
welche die Differenzmaschine nur für Werte von n bis zu 7 tabelliert. Im hier vorliegenden Fall würden die Karten den Mechanismus veranlassen, folgende Sequenz von Operationen zu tabellieren
in der n jede beliebige Zahl sein kann.
Die Karten haben aber noch nichts mit der Festlegung der spezifischen numerischen Daten zu tun. Sie bestimmen lediglich die zu bewirkenden Operationen, die selbstverständlich auf eine unendliche Vielfalt von speziellen numerischen Werten angewandt werden können, die aber selbst keine definierten numerischen Ergebnisse liefern, bis die numerischen Daten des Problems in die entsprechenden Abteilungen des Mechanismus eingegeben wurden. Im obigen Beispiel wäre der erste, wesentliche Schritt zu einem arithmetischen Ergebnis das Ersetzen der spezifischen Werte für n, sowie für die weiteren Grundwerte, die in die Funktion eingehen.
Lassen Sie uns nun annehmen, dass wir für F zwei komplette Gleichungen vierten Grades zwischen x und y vorgeben. Wir müssen auf den Karten nun die Regeln für die Eliminierung in solchen Gleichungen ausdrücken. Die Maschine würde diesen Regeln nachfolgen und am Ende das Ergebnis der Gleichung für eine Variable ausgeben, wie sie sich aus einer solchen Eliminierung ergibt. Verschiedene Modi der Eliminierung könnten ausgewählt werden und natürlich müssten entsprechende Karten erstellt werden. Der im Folgenden beschriebene Modus ist eine der Möglichkeiten. Die Maschine kann zwei beliebige Funktionen miteinander multiplizieren, wenn sie in folgender Form vorliegen:
Dann nämlich können die beiden Gleichungen nach den Potenzen von y angeordnet werden und die Koeffizienten der Potenzen von y sodann nach den Potenzen von x. Die Eliminierung von y ergibt sich aus den aufeinander folgenden Multiplikationen und Subtraktionen mehrerer solcher Funktionen. In diesem Beispiel, wie auch in allen zuvor beschriebenen entsprechenden Fällen, werden die konkreten numerischen Daten und die numerischen Ergebnisse von einigen Teilen und Vorrichtungen des Mechanismus ermittelt, die weitgehend unabhängig von dem Teil sind, welcher die Operationen festlegt.
Beim Studium der Funktionsweise der Analytischen Maschine sehen wir, dass die besondere und unabhängige Natur der Denkweise, mit der in der mathematischen Analysis die Operationen getrennt sind von den von Operationen betroffenen Objekten sowie den Ergebnissen, welche durch diese Operationen erreicht werden, sich bei der Maschine auffallend deutlich und abgetrennt wiederfindet.
Die Aufmerksamkeit auf diesen Punkt zu lenken ist nicht nur deshalb angemessen, weil seine volle Würdigung essenziell für jedes gerechte und angemessene Gesamtverständnis der Leistungen und Betriebsarten der Analytischen Maschine ist, sondern auch deshalb, weil ihm vielleicht generell zu wenig Beachtung beim Studium der mathematischen Wissenschaften geschenkt wird. Er ist andererseits nicht zu verwechseln mit anderen Betrachtungen, die wir beim Verfolgen der Art und Weise anstellen, in der die Maschine ihre Ergebnisse erzielt, oder die bei der Vorbereitung der Daten zur Erlangung dieser Ergebnisse notwendig werden. Es wäre sehr wünschenswert, dass wenn mathematische Prozesse durch den menschlichen Verstand, statt durch das Medium eines toten Mechanismus liefen, es von gleicher Wichtigkeit für diese Dinge wäre, den Schlussfolgerungen im Bezug auf Operationen einen ebenso angemessenen und wohldefinierten Zweig im Gerüst der Analysis einzuräumen, einer fundamentalen und dennoch unabhängigen Zutat der Wissenschaften, die sie beim Studium der Maschine innehaben müssen. Die Verwirrungen, die Schwierigkeiten und die Widersprüche, die als Folge erwünschter klarer Unterscheidungen in diesen Dingen passieren, sind bis vor kürzerer Zeit noch in all den mathematisch belasteten Bereichen aufgetreten, welche negative und unmögliche Größen berücksichtigen. Dies wird auch dem wenig in dieser Wissenschaft bewanderten Leser schnell klar sein und würde allein schon als Grund dafür genügen, diesem Punkt seinen Raum in Verbindung mit einer so passenden Gelegenheit einzuräumen, wie sie notwendigerweise bei der Beschreibung der Analytischen Maschine gegeben ist. Es mag wünschenswert sein zu erläutern, dass wir mit dem Wort Operation hier jeden Prozess meinen, der die wechselseitige Beziehung von zwei oder mehr Dingen betrifft, welcher Art auch immer diese Beziehungen sein mögen. Dies ist die allgemeinste Definition und sie würde alle Dinge des Universums einschließen. In der abstrakten Mathematik verändern Operationen selbstverständlich die konkreten Beziehungen, die bei den Betrachtungen von Zahlen und Räumen beteiligt sind und die Ergebnisse der Operationen sind die speziellen Ergebnisse, die mit der Natur der Subjekte der Operationen korrespondieren. Die Wissenschaft der Operationen jedoch, wie sie speziell von der Mathematik abgeleitet werden, ist eine eigenständige Wissenschaft und sie hat ihre eigenen abstrakten Wahrheiten und Werte; genau so wie die Logik ihre eigenen Wahrheiten und Werte besitzt, ganz unabhängig von den Subjekten, auf welche wir ihre Erkenntnisse und Regeln anwenden mögen. Diejenigen unter Ihnen, die mit einigen der moderneren Ansichten des oben angesprochenen Themas vertraut sind, werden wissen, dass wenn einige fundamentale Beziehungen wahr sind, daraus andere Kombinationen von Beziehungen notwendigerweise folgen müssen; diese Kombinationen sind unbegrenzt in ihrer Vielfalt und Reichweite, wenn die Herleitungen aus den primären Beziehungen nur weit genug fortgeführt werden. Denjenigen wird ebenso bewusst sein, dass einer der Hauptgründe dafür, dass die unabhängige Natur der Wissenschaft der Operationen kaum wahrgenommen wurde und dass ihr allgemein zu wenig Raum gegeben wurde, in der Verschiebung der Bedeutung vieler der in der mathematischen Notation benutzten Symbole liegt. Zunächst sind die Symbole für Operationen oftmals ebenfalls die Symbole für die Ergebnisse der Operationen. Wir könnten sagen, dass diese Symbole geeignet sind, sowohl retrospektive, wie auch ein prospektive Signifikanz zu zeigen. Sie können entweder Beziehungen bezeichnen, die die Folge einer Reihe von bereits ausgeführten Prozessen sind, oder sie bezeichnen Beziehungen, die noch durch bestimmte Prozesse erwirkt werden sollen. Zweitens sind Ziffern, die Symbole der numerischen Größe, oftmals ebenfalls Symbole für Operationen, wenn sie beispielsweise als Indizes für die Potenzen auftreten. Wann immer Begriffe eine wechselnde Bedeutung haben, sind unabhängige Gruppen von Betrachtungsweisen für eine Komplizierung verantwortlich und Beweisführungen sowie Ergebnisse werden oft verfälscht. In der Analytischen Maschine werden nun die Operationen, die unter die erste der oben erwähnten Überschriften fallen, durch eine eigene Notation exklusiv einer für sie zuständigen Abteilung des Mechanismus zugewiesen und dort kombiniert. Im Bezug auf die zweite Überschrift werden Zahlen, wann immer sie Operationen und nicht Größen bezeichnen (so wie die Indizes von Potenzen) auf einer beliebigen Spalte oder auf einer Gruppe von Spalten eingetragen, die Spalten agieren direkt und in gänzlich separater und unabhängiger Weise und sie werden ausschließlich mit dem Operationsmechanismus verbunden und reagieren nur auf diesen. Sie treten niemals in einer Kombination mit einer eine Größe bezeichnenden Zahle aus irgendeiner anderen Spalte auf. Außer natürlich in dem Fall, wenn es sich um Zahlen bei Operationen mit n Spalten handelt, wo diese miteinander kombiniert werden und dies wird oftmals so notwendig sein, genauso wie Größen bezeichnende Zahlen miteinander in jeder Weise kombiniert werden können. Die Ausführung der Maschine hätte so angelegt werden können, dass alle Zahlen, deren Bedeutung eine Operation ist, in einem ganz anderen Bereich der Maschine erschienen wären wie die Zahle, die eine Größe bezeichnen, aber der gegenwärtige Aufbau ist in einigen Fällen einfacher und bietet in der Praxis eben so viel Unterscheidbarkeit, wenn er verstanden wurde.
Der Operationsmechanismus kann sogar unabhängig von jeglichen Objekten, die zu bearbeiten wären, in Gang gesetzt werden (obwohl er dann natürlich kein Ergebnis entwickeln kann). Er könnte ebenso mit ganz anderen Dingen als Zahlen arbeiten, wenn man Objekte finden würden, deren grundlegende gegenseitige Beziehungen durch die abstrakte Wissenschaft der Operationen darstellbar wären und die gleichzeitig empfänglich für abgewandelte Aktionen in der Notation der Operationen und des Mechanismus der Maschine wären. Wenn beispielsweise die fundamentalen Beziehungen der Tonhöhen in der Wissenschaft der Harmonie und der musikalischen Komposition solchen Ausdrücken und Adaptionen zugänglich wären, so könnte die Maschine ausgefeilte und wissenschaftlich fundierte Musikstücke jedweder Komplexität und Länge komponieren.
Die Analytische Maschine ist eine Verkörperung der Wissenschaft der Operationen mit einer besonderen Referenz zu den abstrakten Zahlen als Subjekte dieser Operationen. Die Differenzmaschine ist die Verkörperung einer speziellen Auswahl mit einer sehr beschränkten Zahl von Operationen, die (s.a. die in Notiz B genutzte Notation) somit als (+,+,+,+,+,+) oder auch 6(+) ausgedrückt werden könnte. Sechs Wiederholungen der einen Operation, +, sind tatsächlich die Summe der Funktionalität dieser Maschine. Sie hat sieben Spalten und eine Zahl in irgendeiner der Spalten kann sich selbst zur Zahl der rechts danebenliegenden Spalte addieren. Beginnend mit der am weitesten links liegenden Spalte können so sechs Additionen ausgeführt werden und das Ergebnis erscheint in der siebten Spalte, welche die letzte auf der rechten Seite ist. Der arbeitende Mechanismus dieser Maschine agiert dabei in genauso separater und unabhängiger Weise, wie der der Analytischen Maschine. Da er aber lediglich eine einzige unveränderliche und beschränkte Kombination unterstützt, gibt er wenig Anlass oder Gelegenheit für eine Beschreibung der Unterschiede von Operationen in der Wissenschaft der Operationen. Die Notwendigkeit, die Analytische Maschine von diesem Standpunkt aus zu betrachten wird, wie wir meinen, dem Leser mehr und mehr offenbar werden, wenn er L. M. Menabreas klaren und meisterlichen Artikel weiter verfolgt. Der Kalkulus der Operationen ist gleichsam in sich selbst ein so interessantes Thema und wurde in den letzten Jahren so viel häufiger beschrieben und bedacht als zuvor, dass jede Möglichkeit, die diese Maschine mit ihren Betriebsarten zur Erläuterung dieses Zweiges der mathematischen Wissenschaften bieten kann, nicht übersehen werden sollte. Ob der Erfinder der Maschine auch nur einige dieser Ansichten im Sinn hatte, während er die Erfindung ausarbeitete, oder ob er sie nach dieser Phase je in Betracht zog, das wissen wir nicht. Die Ansichten erschienen uns jedoch zwangsläufig bei zunehmender Vertrautheit mit den Methoden, durch welche die analytischen Kombinationen dieses Mechanismus in der Praxis erreicht werden. Wir können nicht umhin, ein praktisches Ergebnis vorzuschlagen, das uns durch die unabhängige Art, mit der die Maschine ihre Operationen anordnet und kombiniert, wesentlich erleichtert erscheint: wir möchten die Art von Kombinationen andeuten, in die imaginäre Größen Einzug halten. Wir hatten keine Gelegenheit, zu diesem Bereich von Abläufen in der Maschine weitere Nachforschungen anzustellen und unsere Annahme ist sehr wahrscheinlich nicht übereinstimmend mit den Fakten, da das Prinzip, auf denen sie nach unserer Einschätzung beruhen könnte, weniger nützlich als einige andere Prinzipien sein könnte oder doch wenigstens die Mitwirkung anderer Prinzipien erfordern würde. Es erscheint uns aber nichtsdestotrotz offensichtlich, dass es, mit Hilfe einiger einfacher Maßnahmen und durch Erweiterungen im Aufbau des Mechanismus, leicht sein müsste, eine doppelte Gruppe von Ergebnissen auszugeben, so dass wir: Erstens die numerischen Größen als Ergebnis der Operationen mit numerischen Daten erhalten (solche Resultate sind die primäre Aufgabe der Maschine) und zweitens symbolische Resultate, die an den numerischen Resultaten angehängt wären, wobei diese symbolischen Resultate nicht weniger die notwendigen und logischen Konsequenzen von Operationen mit symbolischen Daten sind, wie die numerischen Resultate solche der numerischen Daten.
Wenn wir die Leistungen und die Konstruktionsprinzipien der Differenzmaschine und der Analytischen Maschine miteinander vergleichen, dann werden wir sehen, dass die Möglichkeiten letzterer unmessbar viel weitgehender als die ersterer sind und dass sie tatsächlich zueinander in demselben Verhältnis stehen, wie die Analysis zur Arithmetik. Die Differenzmaschine kann nur eine einzige Abfolge von Operationen bewirken, nämlich die zur Tabellierung des Integrals der speziellen Funktion
und da sie dies nur für Werte von n bis zu 7 ermöglicht, kann sie schon nicht als allgemeinste Umsetzung für auch nur eine spezielle Funktion angesehen werden und erst recht nicht als Umsetzung jeder beliebigen Funktion jeglichen beliebigen Grades. Die Differenzmaschine kann tatsächlich (wie bereits teilweise erläutert wurde) nichts weiter als addieren und jeder andere Vorgang, wie eine simple Subtraktion, Multiplikation oder Division, kann von ihr nur in dem Umfang ausgeführt werden, in dem es möglich ist, den Vorgang auf eine Folge von Additionen zu reduzieren. Die Methode der Differenzen ist tatsächlich eine Methode der Additionen und da sie einfach durch die Addition eine größere Anzahl von Resultaten ermöglicht, als ein anderes mathematisches Prinzip, war diese Funktion als Grundlage für eine Additionsmaschine sehr sinnvoll ausgewählt, weil so die größtmögliche Leistungsfähigkeit einer solchen Maschine zu erreichen war. Im Gegensatz dazu kann die Analytische Maschine gleicht gut entweder addieren, subtrahieren, multiplizieren oder dividieren und sie führt jede dieser vier Operationen in direkter Weise aus, ohne die Mithilfe einer der anderen drei. Diese Tatsache beinhaltet alles und es ist kaum nötig zum Beispiel darauf hinzuweisen, dass die Differenzmaschine lediglich tabellieren kann und nicht in der Lage ist zu entwickeln, währen die Analytische Maschine sowohl tabellieren als auch entwickeln kann.
Die erstgenannte Maschine ist von ihrer Art her eine strikt arithmetische und die Ergebnisse, die sie erreichen kann, liegen in einem klar definierten und begrenzten Bereich, während es für die Analytische Maschine keinerlei ihre Leistungen begrenzende, endgültige Demarkationslinie gibt. Die Leistungen sind gleich auf mit unserem Wissen über die Gesetze der Analysis selbst und daher nur begrenzt durch unsere Vertrautheit mit letzterer. Wir können die Maschine tatsächlich als materiellen und mechanischen Repräsentanten der Analysis ansehen und sehen, dass die Leistungsfähigkeit des menschlichen Studiums in diesem Bereich in viel effektiverer Weise als je zuvor mit unserem theoretischen Wissen über die Prinzipien und Gesetze Schritt halten kann, weil die Maschine uns die vollständige Kontrolle über die auszuführenden Manipulationen an algebraischen und numerischen Symbolen gibt.
Derjenige unter Ihnen, der in der Wissenschaft der Mathematik nicht nur eine Verkörperung abstrakter und unveränderlicher Wahrheiten sieht, deren innere Schönheit, Symmetrie und logische Vollständigkeit, miteinander zu einem Ganzen verbunden, sie zu einem bevorzugten Ort für die Interessen eines jeden tiefgründigen und logisch denkenden Geistes machen, sondern sich auch daran erinnert, sie als den Sprecher einer für die menschliche Rasse noch vorrangigeren Sprache, durch welche wir allein in der Lage sind, die großartigen Fakten der natürlichen Welt angemessen auszudrücken, sowie die unaufhörlichen Veränderungen der in den uns umgebenden Erscheinungen konstant stattfindenden, sichtbaren wie unsichtbaren, bewussten wie unbewussten, wechselseitigen Beziehungen: wer also die mathematische Wahrheit als das Instrument ansieht, durch das der schwache menschliche Geist in effektivster Weise die Schöpfung verstehen kann, der wir mit speziellem Interesse all die Dinge verfolgen, die eine Übersetzung ihrer Prinzipien in eine konkrete, praktische Form zu ermöglichen den Anschein haben.
Die abweichende Charakteristik der Analytischen Maschine, wie auch diejenige, die es zunächst erlaubte, solch weitgehende Möglichkeiten wie die Mechanismen für gerechtfertigte Entscheidungen in ihr zu verwirklichen und sie so zur ausführenden rechten Hand der abstrakten Algebra zu machen, ist die Einführung desselben Prinzips, das Jacquard für die durch Lochkarten ermöglichte Steuerung in der Herstellung von Brokat-Stoffen mit höchst komplizierten Mustern entwickelte. Hierin liegt der Unterschied zwischen den beiden Maschinen. In der Differenzmaschine existiert nichts vergleichbares. Wir könnten treffend schreiben, dass die Analytische Maschine algebraische Muster webt, so wie der Jacquard-Webstuhl Blumen und Blätter webt. Hierin scheint uns wesentlich mehr Originalität zu liegen, als der Differenzmaschine gerechter Weise zugeschrieben werden kann. Wir möchten letzterer nicht jegliche Originalität absprechen. Wir glauben, dass sie den einzigen Vorschlag oder Versuch darstellt, eine rechnende Maschine zu konstruieren, die auf dem Prinzip der aufeinander folgenden Differenzen beruht und die in der Lage ist, ihre eigenen Ergebnisse auszudrucken. Wir glauben, dass diese Maschine ihre Vorgänger sowohl im Umfang der mit ihr möglichen Berechnungen weit hinter sich lässt, als auch in der Leichtigkeit, Sicherheit und Genauigkeit, mit der sie diese Berechnungen ausführt, ohne während der Ausführung der Berechnungen den Eingriff durch einen intelligenten Menschen zu erfordern. Ihre Aufgabe ist aber strengt begrenzt auf die Arithmetik und weit davon entfernt, das erste oder einzige Schema zur Konstruktion von arithmetischen Rechenmaschinen, mit mehr oder weniger Erfolg, zu sein.
Die Grenzen der Arithmetik wurden jedoch in dem Moment gesprengt, als die Idee von den Karten Einzug hielt und die Analytische Maschine hat mit den gewöhnlichen „Rechenmaschinen” nicht viel gemein. Sie belegt eine ganz neue Kategorie und die Gedankengänge, die sie anregt, sind von sehr interessanter Natur. Durch die Schaffung eines Mechanismus, der die Kombination allgemeiner Symbole in Folgen unbegrenzter Vielfalt und unendlichen Umfangs erlaubt, wird eine Verbindung zwischen den rein mechanischen Vorgängen und den theoretischen gedanklichen Prozessen des abstraktesten Bereiches der Mathematik geknüpft. Für die zukünftige Nutzung der Analysis wird eine neue, umfangreiche und leistungsfähige Sprache entwickelt, welche es ermöglicht, ihre Wahrheiten so zu handhaben, dass weit schnellere und korrektere praktische Anwendungen für die Lösung von Aufgaben der Menschheit möglich sind, als sie je zuvor möglich waren. So werden also nicht nur das Geistige und das Materielle, sondern auch das Theoretische und das Praktische aus der Welt der Mathematik in eine intime und effektive Verbindung miteinander gebracht. Uns ist keine Veröffentlichung eines zuvor ausgearbeiteten, oder auch nur gedachten, vergleichbaren Vorschlages bekannt, der wie die Einzelheiten der Analytischen Maschine in so trefflicher Weise geeignet wäre, die Idee einer denkenden oder beweisführenden Maschine in die Praxis umzusetzen.
Wir wenden uns nun einem weiteren Punkt zu, der ein wichtiges Unterscheidungsmerkmal in den Betriebsarten der Differenzmaschine und der Analytischen Maschine ausmacht. Damit erstere ihre Aufgaben erledigen kann, ist es nötig, in ihren Spalten eine Folge von Differenzen der ersten Zahlen einzutragen, die eine jeweils zu untersuchende Tabelle ausmachen. Die Maschine arbeitet dann mit diesen Zahlen als Daten, doch müssen diese Daten selbst zuvor bereits durch eine Reihe von Berechnungen im Kopf eines Menschen ermittelt worden sein. Daher kann diese Maschine nur solche Resultate liefern, die von Daten abhängen, welche andersartig sind und die aus Vorgängen außerhalb des Bereiches ihrer Fähigkeiten herrühren. Es muss, mit anderen Worten, zuvor eine untersuchender Vorgang von einem menschlichen Verstand durchlaufen worden sein um die Daten zu erhalten, auf Grund derer die Maschine dann ihre Resultate synthetisiert. Die Differenzmaschine ist von ihrem Charakter her ausschließlich synthetisierend, während die Analytische Maschine in gleicher Weise zur Analyse, wie auch zur Synthese fähig ist.
Es ist wohl wahr, dass die Differenzmaschine in einem wesentlich größeren Umfang Resultate aus wenigen vorgegebenen errechnen kann, als diese Daten Berechnungen für ihre Ermittlung benötigten. Die Tabelle der Quadratzahlen kann beispielsweise in jedem beliebigen Umfang berechnet werden, wenn nur die Zahlen Eins und Zwei eingestellt sind. Auch würden einige, wenige für irgendeinen Teil der Logarithmentabelle berechnete Differenzen der Maschine genügen, um daraus viele hunderte oder gar tausende von Logarithmen zu berechnen. Und doch macht der Umstand, dass sie nur nachdem jegliche gewählte Funktion zuvor immer numerisch berechnet wurde, sie in ihrer Art und in ihren Vorteilen zweitklassig im Vergleich mit einer Maschine, die, wie die Analytische Maschine, es lediglich erfordert, dass wir die Abfolge und die Verteilung der auszuführenden Operationen kennen, ohne dass wir einen speziellen Fall für genau diese oder auch irgendwelche Operationen zunächst durchgehen müssten, bloß um die Daten zu erhalten, die sie als Voraussetzung benötigen würde. Es müssen natürlich auch numerische Daten eingegeben werden, aber dies sind frei wählbare Daten, nicht etwa Daten, die nur durch eine systematische Reihe von zuvor notwendigen numerischen Berechnungen zugänglich wären, was eine ganz andere Sache ist.
Hierauf könnte eine Antwort sein, dass sehr wohl ein Analyseprozess durchgeführt werden muss, damit die Analytische Maschine mit den notwendigen Operationsdaten ausgestattet werden kann und dass hierin eine mögliche Fehlerquelle liegt. Wenn wir zugestehen, dass der eigentliche Mechanismus seine Aufgabe fehlerfrei erledigt, könnten dennoch die Karten falsche Anweisungen vorgeben. Das ist fraglos richtig, doch stellt es eine viel kleinere Fehlerquelle dar und ist gleichzeitig mit viel weniger Zeit und Arbeit verbunden, wenn lediglich die Operationen und ihre Abfolge bestimmt werden müssen, als wenn auch die numerischen Ergebnisse zu errechnen sind. Im Fall der Analytischen Maschine müssen wir einerseits einen gewiss großen Aufwand an analytischer Arbeit leisten, können aber andererseits einen wesentlich höhere Ersparnis bei den Ergebnissen erhalten. Wir sollten uns auch daran erinnern, dass die Karten, die so allgemein gültig sind wie die Algebra, wenn sie einmal für irgendeine Formel erstellt wurden eine unendliche Zahl von speziellen Fällen abdecken.
Wir sind detailliert auf die unterschiedlichen Feinheiten dieser beiden Maschinen eingegangen weil wir es für wesentlich halten, dass sich ihre jeweiligen Attribute vor einer Wahrnehmung in der Öffentlichkeit deutlich abzeichnen und wir haben daher die vollständig andere Art der Prinzipien, auf denen jede beruht, klar und akkurat dargelegt um es dem Leser offenbar zu machen (wenigstens dem mathematisch bewanderten), in welcher Art und in welchem Umfang die Leistung der Analytischen Maschine diejenige einer Maschine übersteigt, die, wie die Differenzmaschine, lediglich Resultate als die Ergebnisse einer einzigen, bestimmten und eingeschränktem Folge von Abläufen liefern kann, so wie die der Gleichung ![]() . Wir halten dies für wichtig, weil wir wissen, dass in den Köpfen vieler Personen zu diesem Thema häufig nur vage und ungenaue Vorstellungen existieren. Es gibt oft eine nebulöse Erinnerung unter denjenigen, die es überhaupt wahrgenommen haben, dass nacheinander zwei "Rechenmaschinen" von ein und derselben Person in den letzten paar Jahren erfunden wurden, während andere wiederum bisher lediglich von der ursprünglichen "Rechenmaschine" gehört haben und ihnen Erweiterungen nicht bekannt sind. Für jede der beiden Gruppen von Personen sind die zuvor gemachten Überlegungen zutreffend. Während letztere das Faktum der Existenz zweier solcher Maschinen wissen sollten, benötigen erstere nicht weniger akkurate und wohldefinierte Informationen über das Thema. Es existieren bisher keine klaren und korrekten Angaben zu den Charakteristika der Maschinen oder zu ihren jeweiligen Vor- und Nachteilen und durch die mehr oder weniger direkten, zufälligen Berührungen mit diesen Maschinen in vielen Publikationen dieser Tage wird häufig ein Zweifel auftreten, welche "Rechenmaschine" jeweils gemeint war oder ob beide in der Erwähnung enthalten sind.
. Wir halten dies für wichtig, weil wir wissen, dass in den Köpfen vieler Personen zu diesem Thema häufig nur vage und ungenaue Vorstellungen existieren. Es gibt oft eine nebulöse Erinnerung unter denjenigen, die es überhaupt wahrgenommen haben, dass nacheinander zwei "Rechenmaschinen" von ein und derselben Person in den letzten paar Jahren erfunden wurden, während andere wiederum bisher lediglich von der ursprünglichen "Rechenmaschine" gehört haben und ihnen Erweiterungen nicht bekannt sind. Für jede der beiden Gruppen von Personen sind die zuvor gemachten Überlegungen zutreffend. Während letztere das Faktum der Existenz zweier solcher Maschinen wissen sollten, benötigen erstere nicht weniger akkurate und wohldefinierte Informationen über das Thema. Es existieren bisher keine klaren und korrekten Angaben zu den Charakteristika der Maschinen oder zu ihren jeweiligen Vor- und Nachteilen und durch die mehr oder weniger direkten, zufälligen Berührungen mit diesen Maschinen in vielen Publikationen dieser Tage wird häufig ein Zweifel auftreten, welche "Rechenmaschine" jeweils gemeint war oder ob beide in der Erwähnung enthalten sind.
Wir sind gleichermaßen daran interessiert, zwei Missverständnisse auszuräumen, die bis zu einem gewissen Grade mit diesen Maschinen verbunden sind. Zunächst wird weithin angenommen, dass die Differenzmaschine, nachdem sie bis zu einem gewissen Grade fertiggestellt war, die Idee zur Analytischen Maschine geliefert habe und dass letztere tatsächlich ein Nachkomme ersterer sein und aus der Existenz der Vorgängerin durch einige natürliche oder sonst wie zufällige Gedanken, die von dieser nahe gelegt worden seien, geboren wäre. Diese Annahme ist jedoch ganz genau entgegen der Fakten, obwohl sie eine offensichtliche Folge zu sein scheint, wenn zwei in ihrer Natur und Aufgabe so ähnliche Erfindungen in so einem kurzen Zeitabstand und mit so auffälliger Ausweitung der Anwendbarkeit aufeinander folgen, speziell wenn dasselbe Individuum der Autor beider Maschinen ist. Dennoch ergaben sich die Ideen, die zur Analytischen Maschine führten, in einer von denen, die mit der Differenzmaschine verbunden sind, völlig unabhängigen Weise. Die diesen Ideen sind, von der ihnen innewohnenden Natur her, tatsächlich unabhängig von letztgenannter Maschine und hätten sich ebenso gut ergeben können, ohne deren Existenz und ohne einen einzigen Gedanken an sie.
Das zweite der oben erwähnten Missverständnisse bezieht sich auf die wohl bekannte Verzögerung im Fortschritt der Konstruktion der Differenzmaschine über einige Jahre hinweg. Die Umstände respektierend, welche die eigentliche Fertigstellung beider Erfindungen störten, vertreten wir keine Meinung hierzu und selbst wenn wir es wollten, fehlten uns die dazu nötigen Informationen. Wir wissen jedoch, dass einige Personen annehmen, dass die Hürden (wie auch immer sie aussehen) eine Folge der späteren Erfindung der Analytischen Maschine waren, während die vorherige sich noch in der Entwicklung befand. Wir haben selbst manche darüber Lamentieren hören, ob überhaupt eine Idee darin liege, lediglich etwas zu verfolgen, was im Rahmen einer erfolgreichen Ausführung bereits umgesetzt wäre, ohne die Stelle der überlegenen Erfindung einzunehmen. Diese Auffassung können wir nur widersprechen, da sie unqualifiziert ist. Die Fortschritte bei der Differenzmaschine waren schon lange vor dem ersten Aufblitzen von Ideen zu jeglicher ihr überlegenen Erfindung ausgesetzt. Solche Geistesblitze und deren Weiterentwicklung waren in keiner Weise der eigentliche Grund für dieses Aussetzen, obwohl es bei nachweislich existierenden Schwierigkeiten der einen oder anderen Art wahrscheinlich nicht für problemlösend oder auch nur förderlich anzusehen war, dass während ihres Auftretens eine Erfindung durchdacht wurde, die, während sie alles enthielt, was die vorherige vermochte, eine Alles in den Schatten stellende Leistungsfähigkeit besaß.
Wir überlassen es der Entscheidung jedes Einzelnen (nachdem er über kompetente Informationen zu den Charakteristika beider Maschinen verfügt) festzustellen, inwiefern ein solcher Zugewinn für die Leistungsfähigkeit der menschlichen Wissenschaften ein zu entschuldigender Beitrag sei, selbst wenn er (was wir stark bezweifeln) bis zu einem gewissen Grade zu bereits bestehenden Schwierigkeiten beigetragen hat, die bei der Beendigung einer wertvollen, jedoch geringeren Arbeit auftraten. Wir überlassen es jedem, sich selbst an der Weisheit zu ergötzen, die darin läge, sich eine Vernichtung (wäre sie jetzt noch möglich) aller Rekorde einer perfekteren Erfindung zu wünschen, nur um die vergleichsweise beschränkte Erfindung beenden zu können. Die Differenzmaschine würde zweifellos all die praktischen Aufgaben, auf deren Lösung sie ursprünglich ausgerichtet war, erfüllen. Sie würde sicherlich all die Tabellen berechnen, die in direkter Weise für die praktischen physikalischen Aufgaben des Alltags notwendig sind, wie etwa nautische und andere Berechnungen. Wer zu streng utilitaristischen Ansichten neigt, sieht vielleicht die besonderen Leistungen der Analytischen Maschine sich mehr auf Fragen der abstrakten und spekulativen Wissenschaften auswirken, als auf solche, die alltägliche und gewöhnliche menschliche Interessen abdecken. Da solche Personen wahrscheinlich wenig Sympathie, oder gar Vertrautheit, mit jeglichen Bereichen der Wissenschaften verbindet, die sie nicht für nützlich halten (nach ihrer Definition dieses Wortes), könnten sie nun der Meinung sein, dass die Realisierung dieser Maschine, nachdem die neuere bereits in Entwicklung ist, eine unfruchtbare und unproduktive Verschwendung von noch mehr Geld und Arbeit sei, tatsächlich eine Arbeit von Mehrleistung. Selbst unter utilitaristischen Gesichtspunkten zweifeln wir jedoch nicht daran, dass sehr wertvolle praktische Resultate mit den erweiterten Möglichkeiten der Analytischen Maschine erreicht würden, darunter manche Ergebnisse, auf die wir denken hinweisen zu können, hätten wir nur genügend Platz, sowie andere, die derzeit noch unvorhersehbar sein mögen, die jedoch durch die täglich wachsenden Erfordernisse der Wissenschaft und durch eine intimere praktische Vertrautheit mit den Leistungen der Maschine, wäre sie bereits jetzt verfügbar, befördert würden.
Im Allgemeinen sehen wir in beidem, sowohl in einer a priori Beschreibung, wie auch in einer auf der wissenschaftlichen Geschichte und Erfahrung der Menschheit beruhenden, eine starke Annahme dafür, dass dies der Fall wäre. Dennoch werden wahrscheinlich alle dem Gefühl zustimmen, dass eine Fertigstellung der Differenzmaschine weit mehr zu wünschen wäre, als ein Nicht beenden jeglicher Rechenmaschine überhaupt. Wer oder was auch immer für die Ursachen der Schwierigkeiten, die offenbar entweder bei der Fertigstellung der früheren Maschine oder den Anfängen der neueren bestehen, die Ursache sein mag, wir vertrauen darauf, dass er oder es nicht letztendlich verhindern wird, dass unsere Generation mit diesen Erfindungen wenigstens durch das Medium von Feder, Tinte und Papier eine Vertrautheit erlangt. Und noch mehr hoffen wir, dass zur Ehre des Ansehens unseres Landes auf den Seiten der Geschichtsbücher der Zukunft, diese Ursachen nicht dazu führen, dass eine andere Nation oder Regierung diese Unternehmung abschließt. Dies wäre nicht zu entschuldigen, unabhängig davon, ob die Hürden ihre Ursache in privaten Interessen und Gefühlen haben, im Nachdenken über eine öffentlich zugänglichere Beschreibung oder in Gründen, die in der Natur von beiden dieser Lösungen liegen.
Wir verweisen den Leser für eine sehr treffende Beschreibung der Differenzmaschine auf den "Edinburgh Review" vom Juli 1834. Der Schreiber dieses Artikels hat einen gänzlich anderen Aspekt als Anlass für diese Veröffentlichung hervorgehoben, als L. M. Menabrea ihn gewählt hat. Ersterer behandelt die Maschine hauptsächlich unter ihren mechanischen Gesichtspunkten und geht dabei nur kurz auf die mathematischen Prinzipien ein, die diese Maschine repräsentiert, während er viele Details des Mechanismus und der Vorrichtungen, mit deren Hilfe die Maschine die verschiedenen Grade der Differenzen tabelliert, in deutlicher Länge angibt. L. M. Menabrea entwickelt hingegen ausschließlich die analytische Sichtweise und setzt voraus, dass der Mechanismus bestimmte Prozesse ausführen kann, ohne den Versuch zu machen, wie sie funktionieren. Vielmehr leitet er die ganze Aufmerksamkeit auf Erklärungen und Illustration zu der Art und Weise, in der analytische Gesetze so formuliert und kombiniert werden können, dass jeder Zweig dieses weiten Bereichs in die Reichweite der angenommenen Leistungsfähigkeit des Mechanismus rückt. Es ist offensichtlich, dass beide Zweige dieser Aufgabe für die Erfindung einer Rechenmaschine gleich wichtig sind und dass jeglicher Fortschritt auf ihren gegenseitigen Abwägung beruhen muss. Sie müssen sich so treffen, dass die Schwachpunkte in der Leistungsfähigkeit in dem einen Bereiches durch starke Punkte im anderen Bereich ausgeglichen werden können. Sie sind untrennbar verbunden, obwohl sie von ihrer inneren Struktur her so unterschiedlich sind, dass ein einziger Verstand wahrscheinlich nicht gleich fundiert oder erfolgreich bei beiden sein kann. Wir kennen die, die bezweifeln, dass die Leistungsfähigkeit des Mechanismus in der Praxis allen an ihn gestellten Anforderungen bei der Bearbeitung solch komplizierter mechanischer Abläufe, wie sie bei beiden Maschinen auftreten, sich als ausreichend erweisen wird und die erwarten, dass unvorhersehbare praktische Schwierigkeiten und Verwirrungen auf dem Weg hin zur Korrektheit und Einsetzbarkeit der Maschinen auftreten werden. Die Differenzmaschine scheint uns jedoch eine großartige Antwort auf diese Zweifel zu sein. Sie ist so komplett, wie sie sein kann und erledigt all ihre Aufgaben mit dem vorhersehbaren Erfolg. Die Analytische Maschine ist hingegen nicht nur nicht wesentlich komplizierter, sondern in vielen Bereichen einfacher zu konstruieren und es ergibt sich mit ihr der bemerkenswerte Umstand, dass sie mit ihren viel einfacheren Voraussetzungen eine so viel größere Leistungsfähigkeit liefert.
Der Artikel im "Edinburgh Review" wurde einige Zeit vor dem Auftreten jeglicher Ideen geschrieben, die später zur Erfindung der Analytischen Maschine führten und in den Eigenschaften der Differenzmaschine liegt viel weniger ein Grund, der einen Autoren dazu einladen würde, sich mit ihr exklusiv, oder auch nur vorwiegend, unter mathematischen Gesichtspunkten zu befassen, als dies bei der der Analytischen Maschine der Fall ist, obwohl dieser Mechanismus zweifellos eine viel größere Annäherung an die Mathematik erreicht, als jener der vorgenannten. Eine Veröffentlichung mit einer Beschreibung der mechanischen Aspekte der Analytischen Maschine ist wünschenswert und wird, wie wir hoffen, sehr bald zur Verfügung stehen.
Wer vielleicht die Geduld aufbringt, eine erträgliche Menge von einigermaßen trockenen Details zu studieren, wird nach dem Lesen des Artikels von 1834 eine angemessene Entschädigung durch die Klarheit und die konsequente Sichtweise erhalten, mit der die verschiedenen praktischen Schritte beschrieben werden, durch die der Mechanismus bestimmte Prozesse ausführt und er wird L. M. Menabreas ausführlichere und weitreichendere Denkschrift noch mehr als zuvor zu würdigen wissen. Gerade die Unterschiede im Stil und Themenbereich dieser beiden Artikel machen den einen zu einer wertvollen Ergänzung des jeweils anderen, wenigstens für diejenigen unter Ihnen, die tatsächlich etwas mehr als nur eine übersichtliche und populäre Beschreibung des Themas Rechenmaschinen lesen wollen.
A.A.L.
Die Abteilung der Analytischen Maschine, die hier angesprochen ist, trägt den Namen Speicherhaus. Sie enthält eine nicht festgelegte Anzahl von Spalten mit Scheiben, wie sie L. M. Menabrea beschrieben hat. Wenn der Leser sich ein Bild vorstellt, in dem rechteckige Zählermarkierungen bis zu einer gewissen Höhe aufgestapelt sind, wobei jeder Zähler die Ziffern von 0 bis 9 in gleichen Abständen auf seinem Rand trägt und wenn er weiterhin annimmt, dass diese Zähler nicht so einer auf dem anderen liegen, dass sie miteinander in Kontakt stehen, sondern dass sie mit geringem vertikalen Abstand voneinander auf einer gemeinsamen Achse befestigt sind, die vertikal durch ihre Mittelpunkte geht und um die sich jede Scheibe horizontal drehen kann, so dass jede benötigte Ziffer aus dem Bestand, der auf dem Rand aufgebracht ist, zur Anzeige gebracht werden kann, dann hat er eine gute Vorstellung von einer dieser Spalten. Die unterste der Scheiben einer jeden Spalte beschreibt die Einheiten, die nächste darüber die Zehner, die nächste darüber die Hunderter und so weiter. Wenn wir also die Zahl 1345 in eine Spalte der Maschine eintragen wollen, würde sie so dargestellt:—
In der Differenzmaschine gibt es sieben solcher Spalten, die in einer Reihe nebeneinander angebracht sind und der Arbeitsmechanismus liegt hinter ihnen: das Gesamtbild der Maschinerie ist das eines quadratischen Prisma (das sich mehr oder weniger einem Würfel annähert), wobei die Ergebnisse stets auf der Seitenfläche der Maschine erscheinen, die jene Spalten mit den Scheiben enthält und der gegenüber sich ein Beobachter aufstellen kann. Die Analytische Maschine hätte wesentlich mehr Spalten, vielleicht wenigstens Hundert. Die präzise Form und Anordnung der ganzen Mechanerie der Analytischen Maschine ist noch nicht endgültig festgelegt.
Die Spalten mit den Scheiben ließen sich auf Papier in folgender Weise bequem darstellen:—

Die Vs dienen der bequemen Referenz für eine beliebige Spalte, sowohl schriftlich, als auch mündlich und sie sind fortlaufend nummeriert. Der Grund, weshalb dem Buchstaben V der Vorzug vor jedem anderen Buchstaben gegeben wurde, liegt darin, dass diese Spalten (wie der Leser beim weiteren Studium dieser Denkschrift herausfinden wird) als Variablen bezeichnet werden, manchmal auch als Variablenspalten oder als Spalten von Variablen. Die Herkunft dieser Bezeichnung ist, dass die Werte dieser Spalten sich verändern, also in jeder vorstellbaren Weise variieren. Es ist jedoch notwendig, das sich aufdrängende Missverständnis zu verhindern, dass diese Spalten ausschließlich die Werte der Variablen einer analytischen Formel enthielten und nicht ebenso die der Konstanten. Die Spalten werden aus einem Grund Variablen genannt, der gänzlich unabhängig von der analytischen Unterscheidung zwischen Konstanten und Variablen ist. Um mögliche Verwirrungen zu vermeiden, haben wir sowohl in der Übersetzung, als auch in den Notizen, Variable mit einem großen V geschrieben, wenn das Wort eine Spalte der Maschine bezeichnet, jedoch mit einem kleinen V, wenn wir eine Variable einer Formel meinen. Dementsprechend meint Variablenkarten jegliche Karten, die zu einer Spalte der Maschine gehören.
Um zur Erklärung des Diagramms zurückzukehren: jeder Kreis im oberen Teil ist dafür gedacht, das algebraische Zeichen + oder - zu enthalten, die eingesetzt werden können, je nachdem, ob die in der Spalte darunter dargestellte Zahl positiv oder negativ ist. In ähnlicher weise können andere rein symbolische Ergebnisse von algebraischen Prozessen in diesen Kreisen erscheinen. In Notiz A wurde die Nützlichkeit der wie numerische Ergebnisse eben so einfachen symbolischen Entwicklung von Ergebnissen angerissen. Die Nullen neben den symbolischen Kreisen bezeichnen jeweils eine Scheibe, die eine Ziffer 0 an der Vorderseite darstellen soll. Nur vier Stellen von Nullen sind im Diagramm dargestellt, jedoch können diese als Repräsentanten für dreißig oder vierzig, oder jede beliebige Anzahl von Scheiben, die benötigt wird, angesehen werden. Da jede Scheibe jede Ziffer darstellen kann und jeder Kreis jedes Vorzeichen, können die Scheiben jeder Spalte so eingestellt werden, dass sie jede beliebige positive oder negative Zahl im Bereich der Grenzen der Maschine darstellen können, deren Grenzen von den frontseitigen Ausmaßen der Maschine abhängen, also von der Anzahl der Scheiben einer Spalte.
Jedes der Quadrate unter den Nullen ist gedacht für die Eintragung eines beliebigen Symbols oder einer Kombination von Symbolen, wobei die in der Spalte darüber stehende Zahl den numerische Wert des Symbols oder der Symbolkombination darstellen soll. Lassen Sie uns zum Beispiel die drei Größen a, n und x darstellen und lassen Sie uns weiterhin annehmen, dass a = 5, n = 7 und x = 98 ist. Dann haben wir:—
Wir können diese Symbole nun in verschiedenartigster Weise kombinieren, also etwa eine beliebige Funktion oder mehrere Funktionen mit ihnen bilden und wir können jede dieser Funktionen in Klammern aufschreiben, wobei jede Klammer die Größen (und nur diese Größen) zusammenfasst, die in die unter ihr eingeschriebene Funktion eingehen. Wir müssen ihr weiterhin eine weitere Spalte rechter Hand zuordnen, wenn wir uns für eine bestimmte Funktion entschieden haben, deren numerischen Wert wir berechnen wollen und wir müssen die Funktion in das Quadrat unter dieser Spalte eintragen. Mit den obigen Vorgaben könnten wir jede der folgenden Funktionen wählen:—
Lassen Sie uns die erste auswählen. Sie würde, vor der Berechnung, wie folgt dargestellt:—
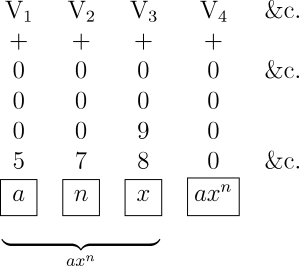
Nachdem die Daten vorgegeben sind, müssen wir nun in die Maschine die Karten eingeben, die die Operationen für diese spezielle ausgewählte Funktion anweisen. Im konkreten Fall wären diese Operationen:—
Zunächst, um xn zu erhalten, sechs Multiplikationen (=987 für die oben angegebenen konkreten Daten).
Zweitens eine Multiplikation, um a·xn zu erhalten (=5·987).
Insgesamt sieben Multiplikationen für den ganzen Vorgang. Wir können sie so repräsentieren:—
Die Multiplikationen würden aber in aufeinander folgenden Stufen während der Lösung des Problems mit Zahlen aus verschiedenen Spalten operieren. Anders gesagt würde dieselbe Operation mit verschiedenen Operatoren ausgeführt. Dies ist ein weiteres Beispiel für die Anmerkungen über die unabhängige Art und Weise, in der die Maschine ihre Operationen ausführt, die in der vorherigen Notiz erläutert wurde. Wenn der Wert von axn ermittelt wird, sind die Operationen homogen, jedoch in den aufeinander folgenden Stufen der Berechnung verteilt über verschiedene Operatoren. Durch bestimmte Lochkarten, die zu den Variablen selbst gehören, wird die Ausführung der Operationen so verteilt, dass sie zur jeweiligen Funktion passen. Die Operationskarten bestimmen lediglich die Abfolge von Operationen im Allgemeinen. Sie führen tatsächlich dazu, dass ein Teil des Mechanismus, der in der Mühle vorhanden ist, in eine Folge von unterschiedlichen Zuständen gebracht wird, die wir jeweils als den Additionszustand, den Multiplikationszustand &c bezeichnen können. In jedem dieser Zustände ist der Mechanismus in der Lage, in der für diesen Zustand typischen Art mit einem beliebigen Paar von Zahlen, die ihm zugänglich gemacht werden können, zu arbeiten. Die Mühle kann nur jeweils einen dieser Operationszustände zu einer Zeit annehmen und die Bauweise des Mechanismus ist so, dass auch nur ein Paar von Zahlen zu einem Zeitpunkt empfangen und bearbeitet werden kann. Um also sicherzustellen, dass die Mühle eine konstante Abfolge von korrekten Zahlenpaaren erhält und dass sie auch das Ergebnis der mit eine beliebigen Paar ausgeführten Operation richtig einträgt, hat jede Variable ihre eigenen, zu ihr gehörenden Karten. Es gibt erstens eine Sorte von Karten, deren Aufgabe darin besteht, die Übertragung des Zahlenwerts einer Variablen in die Mühle zu gestatten. Diese Karten können als die Einlieferungskarten bezeichnet werden. Sie statten die Mühle mit der notwendigen Nahrung aus. Jede Variable hat zweitens eine weitere Sorte von Karten, deren Wirkung darin besteht, dass die Variable eine Zahl von der Mühle empfängt. Diese Karten können als die Empfangskarten bezeichnet werden. Diese Karten Bestimmen die Plätze sowohl der temporären, wie auch der endgültigen Ergebnisse. Es scheint uns, dass die Variablenkarten (beider vorgenannten Sorten) allgemein noch besser als Distributionskarten bezeichnet werden könnten, da mit ihrer Hilfe die Ausführung der Operationen und die Ergebnisse dieser Operationen korrekt verteilt werden.
Es gibt zwei Arten der zugehörigen Variablenkarten, beziehungsweise sind sie für die Erfüllung zweier untergeordneter Aufgaben angepasst. Da diese Modifikationen jedoch nicht zum gegenwärtigen Thema gehören, werden wir an anderer Stelle darauf eingehen.
Im obigen Fall von axn bestimmen die Operationskarten lediglich sieben Multiplikationen, das heisst, sie sorgen dafür, dass die Mühle aufeinander folgend sieben Mal im Multiplikationszustand sein soll (ohne dabei je eine Referenz derjenigen Spalten zu enthalten, mit deren Zahlenwerten operiert werden soll). Die passend verteilenden Variablenkarten wechseln in jeder der aufeinander folgenden Multiplikationen und bestimmen die Distributionsbedingungen für den jeweiligen Fall.
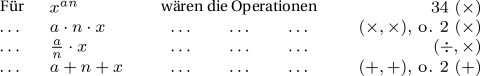
Die Maschine könnte all diese Ergebnisse nacheinander berechnen. Nachdem axn erledigt wäre, könnte die Funktion xan anstatt axn unter die Klammern geschrieben und die neue Berechnung gestartet werden (wobei natürlich die angemessenen Operations- und Variablenkarten für die neue Funktion ins Spiel kämen). Die Ergebnisse erschienen in der Spalte V5. Entsprechendes gelte für jede Funktion der Größen a, n und x. Jedes Ergebnis könnte entweder während der weiteren Berechnungen dauernd in seiner Spalte bleiben, so dass nachdem alle die Funktionen berechnet wurden, ihre Werte gleichzeitig in den Spalten V4, V5, V6, &c. stünden, oder es könnte jedes Ergebnis (nachdem es ausgedruckt wäre oder in einer bestimmten Art genutzt wurde) kopiert werden, um Platz für seinen Nachfolger zu machen. Das Quadrat unterhalb der Spalte V4 müsste für den letztgenannten Weg nacheinander die Funktionen axn, xan, anx, &c. enthalten.
Lassen Sie uns nun annehmen, wir hätten zwei Ausdrücke, deren Werte von der Maschine unabhängig voneinander berechnet worden wären (jeder mit seiner eigenen Gruppe von Spalten für die Daten und Ergebnisse). Nehmen wir axn und bpy. Sie würden dann wie folgt in den Spalten stehen:—

Wir könnten nun jegliche Kombination dieser zwei Ergebnisse wünschen, wobei es nur nötig wäre, eine oder mehrere weitere Karten zu haben, die die notwendigen Anweisungen für die Operationen mit den zwei Ergebnisspalten V4 und V8 geben und das Ergebnis dieser weiteren Operationen in einer neuen Spalte eintragen, etwa in V9. So wollen wir etwa axn durch bpy dividieren. Der numerische Wert dieser Division würde dann in der Spalte V9 erscheinen, unterhalb der wir ![]() eingetragen haben. Die komplette Serie von Operation, von Beginn an, wäre dann wie folgt (für n gleich 7):
eingetragen haben. Die komplette Serie von Operation, von Beginn an, wäre dann wie folgt (für n gleich 7):
Dieses Beispiel ist lediglich angeführt um zu zeigen, dass wir, wenn wir das möchten, beliebige Zwischenergebnisse (wie axn und bpy), die während der Abläufe erscheinen, die ein größeres und komplizierteres Ergebnis (wie ![]() ) als letztes Ziel haben, auch separat und dauerhaft beibehalten können.
) als letztes Ziel haben, auch separat und dauerhaft beibehalten können.
Jede Gruppe von Spalten kann als Darstellung einer allgemeinen Funktion betrachtet werden, die so lange allgemein bleibt, bis eine spezielle implizit dadurch festgelegt wurde, dass weitere Operations- und Variablenkarten für eine bestimmte Funktion in die Maschine eingebracht wurden. Im vorhergehenden Beispiel würden also V1, V2, V3, V5, V6 und V7 die allgemeine Funktion ![]() (a, n, b, p, x, y) bestimmen, bis man sich für die Funktion
(a, n, b, p, x, y) bestimmen, bis man sich für die Funktion ![]() entschieden hat und dies implizit ausdrückt, indem man passende Karten in die Maschine einlegt. Die eigentliche Arbeit des Mechanismus, wie er von diesen Karten reguliert wird, entwickelt dann explizit diesen Funktionswert. Das Notieren einer Funktion unterhalb der Klammern und im Quadrat unter der Ergebnisspalte beeinflusst in keiner Weise die Abläufe oder Ergebnisse und dient lediglich als eine Gedächtnisstütze für den Beobachter, damit er sich erinnert, was gerade geschieht. Die Operations- und die Variablenkarten bestimmen in der Realität allein die Funktion. Man sollte tatsächlich ganz für sich betrachten, dass die Beschreibungen in jeglichem Quadrat ganz unabhängig vom Mechanismus und den Abläufen in der Maschine sind und nichts weiter als dort platzierte, frei wählbare Gedächtnishilfen zur Unterstützung des Bedieners darstellen.
entschieden hat und dies implizit ausdrückt, indem man passende Karten in die Maschine einlegt. Die eigentliche Arbeit des Mechanismus, wie er von diesen Karten reguliert wird, entwickelt dann explizit diesen Funktionswert. Das Notieren einer Funktion unterhalb der Klammern und im Quadrat unter der Ergebnisspalte beeinflusst in keiner Weise die Abläufe oder Ergebnisse und dient lediglich als eine Gedächtnisstütze für den Beobachter, damit er sich erinnert, was gerade geschieht. Die Operations- und die Variablenkarten bestimmen in der Realität allein die Funktion. Man sollte tatsächlich ganz für sich betrachten, dass die Beschreibungen in jeglichem Quadrat ganz unabhängig vom Mechanismus und den Abläufen in der Maschine sind und nichts weiter als dort platzierte, frei wählbare Gedächtnishilfen zur Unterstützung des Bedieners darstellen.
Je länger wir die Art weiter betrachten, in der die Maschine ihre Abläufe durchführt und ihre Ergebnisse erhält, um so mehr werden wir erkennen, welch bezeichnende Licht sie in richtiger und angemessener Weise auf die gegenseitigen Beziehungen und Verbindungen der verschiedenen Schritte der mathematischen Analysis wirft, wie klar sie die Dinge trennt, die auch in der Realität unterschiedlich und unabhängig voneinander sind und wie sehr sie die Dinge vereint, die voneinander abhängig sind.
A.A.L.
Diejenigen Leser, die weitere Prinzipien des Jacquard-Webstuhls in der effizientesten Weise und nicht bloß durch praktische Beobachtung studieren möchten, müssen lediglich die Adelaide-Galerie oder das Polytechnische Institut besuchen. In jeder dieser wertvollen Sammlungen von wissenschaftlichen Illustrationen arbeitet auch immer ein Weber an einem Jacquard-Webstuhl und ist dazu bereit, alle gewünschten Informationen über die Konstruktion und die Betriebsarten seines Apparats zu geben. Der Band über die Herstellung von Seide in Lardner's Cyclopædia enthält ein Kapitel über den Jacquard-Webstuhl, das ebenfalls hilfreiche Hinweise geben kann.
Die Anwendungsmethode der Karten, wie sie bis dato bei der Webkunst eingesetzt sind, wurde jedoch für nicht ausreichend leistungsfähig gehalten, um all die Vereinfachungen in den vielfältigen und komplizierten Prozessen zu erbringen, deren Erreichung wünschenswert ist, um die Aufgaben der Analytischen Maschine zu erfüllen. Es wurde eine Methode entwickelt, die technisch als Ablage für Karten in bestimmten Gruppen und nach bestimmten Regeln bezeichnet wird. Die Aufgabe dieser Erweiterung ist es zu gewährleisten, dass jede einzelne Karte, oder jedes Set von Karten, beliebig oft hintereinander zur Lösung eines Problems wiederverwendet werden kann. Ob diese Möglichkeit genutzt wird, oder nicht, hängt in jedem Einzelfall von der Natur der Operationen ab, die das zur Bearbeitung stehende Problem erfordern mag. Dieser Vorgang wird von L. M. Menabrea erwähnt und stellt eine sehr wichtige Vereinfachung dar. Es wurde vorgeschlagen, die Wiederverwendung in solchen Fällen einzusetzen, die, während sie selbst keine offensichtliche Verbindung mit dem Bereich der abstrakten Wissenschaften haben, sich für diese jedoch als sehr wertvoll erwiesen haben, weil sie mit neuen und einzigartigen Anwendungsfeldern Prinzipien für mögliche algebraische Kombinationen nahe legen, welche genauso in den Möglichkeiten des Mechanismus enthalten sind, wie all die verschiedenen Feinheiten, die bei sich überschneidende Fäden auftreten können. Durch die Einführung des Ablage-Systems in den Jacquard-Webstuhl selbst könnten Muster, die eine Symmetrie enthalten müssten und gleichförmigen Regeln beliebiger Länge unter lägen, mit vergleichsweise wenigen Karten gewoben werden.
Wer den Mechanismus dieses Webstuhls verstanden hat wird einsehen, dass obige Verbesserung in der Praxis leicht dadurch zu erreichen ist, dass das Prisma, über welches der Zug von Musterkarten hinweg läuft, darauf umgestellt wird, sich rückwärts statt vorwärts zu drehen, je nach Belieben und unter den vorausgesetzten Umständen, bis dabei eine bestimmte Karte oder Gruppe von Karten, die ihre Aufgabe schon einmal erfüllt hatte und in der normalen, regulären Abfolge bereits vorüber gegangen war, auf die Position zurückgebracht wird, die sie direkt vor ihrer vorherigen Nutzung innehatte. Das Prisma stellt danach seine Vorwärts-Rotation wieder ein und bringt so die fragliche Karte, oder die Gruppe von Karten, zum zweiten Mal ins Spiel. Dieser Prozess kann offensichtlich beliebig oft wiederholt werden.
A.A.L.
Wir haben die Lösungen dieser beiden Gleichungen weiter unten in allen Details in einem Diagramm dargestellt, das jenen in Notiz B gleicht, jedoch ist eine weitergehende Erklärung notwendig, zum einen Teil deshalb, um diesen komplizierteren Fall ganz klar zu machen und zum anderen Teil, um das Verständnis bestimmter Indikationen und Notationen zu ermöglichen, die in den vorherigen Diagrammen nicht vor kamen. Speziell denjenigen unter Ihnen, welche die Notiz G vollständig verstehen wollen, sei geraten, besonderes Augenmerk auf den Inhalt der aktuellen Notiz zu legen, oder sie werden den entsprechenden Notationen und Indikationen in einem wesentlich komplizierteren Fall nicht folgen können.
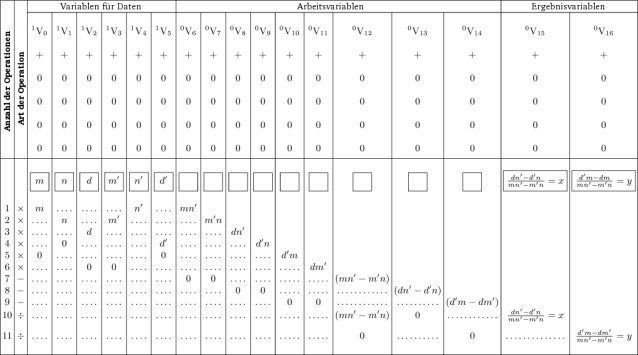
|
| Ein Klick auf das Diagramm zeigt eine größere Darstellung an. Der “Zurück”-Button Ihres Browsers bringt Sie zu diesem Dokument zurück. Eine druckfertige PostScript-Datei dieses Diagramms steht ebenfalls für den Download als komprimiertes ZIP-Archiv zur Verfügung. |
In allen Berechnungen können die Spalten der Variablen in drei Klassen eingeteilt werden:—
1. Spalten, in die Daten eingetragen werden sollen
2. Spalten, die die Endergebnisse empfangen sollen
3. Spalten, die dazu gedacht sind, solche Zwischenergebnisse und Kombinationen von einfachen Daten zu enthalten, die nicht permanent erhalten bleiben sollen, sondern lediglich dazu notwendig sind, um mit ihnen auf dem Weg zu den Endergebnissen weiter arbeiten zu können. Kombinationen von Daten dieser Art könnte man treffend als Sekundärdaten bezeichnen. Es gibt tatsächlich sehr viele aufeinander folgende Stufen bis hin zum endgültigen Ergebnis. Die Spalten, die diese Sekundärdaten empfangen, sind treffend als Arbeitsvariablen bezeichnet, weil ihre Aufgabe ihrer Natur nach ganz untergeordnet unter andere Aufgaben ist. Sie liefern eine vorübergehende und vergängliche Klasse von Ergebnissen, welche die Originaldaten mit den Endergebnissen verbindet.
Die Ergebnisvariablen nehmen manchmal die Gestalt von Arbeitsvariablen an. Es passiert häufiger, dass eine Variable, die ein Endergebnis enthalten soll, während des Ablaufs des Prozesses der Empfänger für ein oder mehrere aufeinander folgende Zwischenergebnisse wird. Entsprechend werden die Variablen für Daten oftmals Arbeitsvariablen oder Ergebnisvariablen, oder gar beides nacheinander. In den aktuellen Gleichungen sind jedoch zufällig die Bereiche dieser drei Gruppen über den gesamten Ablauf hin perfekt voneinander getrennt und unabhängig voneinander.
Man wird später sehen können, dass in den Quadraten unterhalb der Arbeits-Variablen nichts eingetragen ist. Jede dieser Variablen ist in vielen Fällen dafür vorgesehen, während des Ablaufs einer Berechnung verschiedene Werte nacheinander durch zu leiten (obwohl dieser Fall in den hier beschriebenen Gleichungen nicht vorkommt). Es gibt daher konsequenterweise auch nicht nur ein einziges festgelegtes Symbol und keine Kombination von Symbolen, die als lediglich zu einer Arbeits-Variablen zugehörig verstanden werden sollten und als eine allgemeine Regel sind die Quadrate dieser Variablen leer gelassen. Natürlich ist dies so zu verstehen, wie in allen anderen Fällen, in denen eine generelle Regel erwähnt wird, dass im Einzelfall auch Ausnahmen von einer solchen Regel auftreten können.
Damit alle Indikatoren, die im Diagramm enthalten sind, vollständig zu verstehen sind, wollen wir zwei oder drei Punkte erklären, die bis dato nicht angerührt wurden. Wenn der Wert irgendeiner Variablen als in Benutzung bezeichnet wird, dann kann dies eine von zwei möglichen Konsequenzen haben. Entweder kehrt der Wert in die Variable zurück, nach sie genutzt wurde, wodurch sie bei Bedarf für einen weitere Verwendung bereit steht, oder die Variable kann auf Null gesetzt werden. (Wir denken dabei natürlich nicht an einen dritten Fall, der häufig auftauchen wird, in dem dieselbe Variable auch dazu bestimmt ist, das Ergebnis genau der Operation zu enthalten, für die sie gerade eine Zahl geliefert hat.) Die Standardregel ist die, dass der Wert einer Variablen zu ihr zurückkehrt, wenn nicht vorhersehbar ist, dass sich kein weiterer Bedarf für diesen Wert ergeben kann, in welchem Fall die Null eingesetzt würde. Am Ende einer Berechnung sollte daher, als allgemeine Regel, jede Spalte eine Null enthalten, mit Ausnahme der Spalten, die Ergebnisse darstellen sollen. Daher wird man im Diagramm sehen können, dass wenn m - der Wert von V0 - zum zweiten Mal bei Operation 5 genutzt wird, V0 auf 0 gesetzt wird, das m nicht wieder gebraucht wird und das vergleichbar damit, nachdem (mn' − m'n) in V12 in Operation 11 zum dritten Mal genutzt wurde, V12 Null wird, da (mn' − m'n) nicht wieder benötigt wird. Um den einen oder den anderen der oben erwähnten Wege zu beschreiten, gibt es zwei Arten der Eingabe Variablenkarten. Eine dieser Arten hat die Eigenschaft, den Zahlenwert irgendeiner Variablen zu ihr zurückkehren zu lassen, nachdem er ihre Aufgabe in der Mühle erfüllt hat. Die andere Art hat die Eigenschaft, für die gelieferte Zahl die Null in der Spalte der Variablen einzusetzen. Diese zwei Arten werden, wenn das nötig ist, durch die jeweilige Bezeichnung als Erhaltende und als Null Eingabekarten unterschieden. Wir sehen, dass die vorwiegend Aufgabe (siehe Notiz B) der beiden Arten von Karten dieselbe ist, sie unterscheiden sich nur in ihrer zweitrangigen Aufgabe.
Zu jeder Variable gehören demgemäß eine Klasse von Ausgabe-Variablenkarten und zwei Klassen von von Eingabe-Variablenkarten. Es ist jedoch klar, das von letzteren jeweils nur die eine oder die andere für eine Variable in einer Operation genutzt werden kann, nie beide gleichzeitig, da ihre jeweiligen Funktionen zueinander inkompatibel sind.
Es sollte klar sein, dass die Variablenkarten nicht etwa in direkter Weise bei den Spalten platziert werden. Jede Karte ist durch Drähte mit der Spalte verbunden, auf die sie wirken soll.
Unser Diagramm wäre praktischer neben L. M. Menabreas korrespondierender Tabelle platziert worden, damit die Operationen in beiden Zeile für Zeile miteinander verglichen werden könnten. Jedoch war es unglücklicherweise zu unbequem, sie in dieser zu wünschenden Form auszudrucken. Das Diagramm ist vordergründig lediglich eine andere Art und Weise, die in L. M. Menabreas Tabelle beschriebenen verschiedenartigen Relationen darzustellen. Beide Darstellungen haben jeweils einige Vor- und Nachteile. In Kombination stellen sie eine vollständige und akkurate Methode dar, um jeden Schritt und den Ablauf in allen von der Maschine durchgeführten Berechnungen zu notieren.
Bis jetzt wurde den oberen Indizes keine Beachtung geschenkt, die im Diagramm jedem V links hinzugefügt sind. Wir haben uns die Freiheit genommen, diese Indizes auch zu den Vs in L. M. Menabreas Tabellen 3 und 4 hinzuzufügen, da sie nichts von dem verändern, was er darin darstellt, sondern lediglich etwas zu den vorherigen Indizierungen in diesen Tabellenhinzufügen. Die unteren Indizes, deren Werte während des Ablaufs der Berechnungen unverändert fortbestehen, sind offensichtlich nur Indizes für die Zugehörigkeit und gänzlich unabhängig von den durchgeführten Operationen und den Ergebnissen. Die oberen Indizes jedoch sind von anderer Art. Ihre Aufgabe ist es, jede Veränderung des Wertes einer Variable anzuzeigen und sie tragen natürlich die Verantwortung für Veränderungen während der Berechnung. Immer dann, wenn eine Variable nur mit Nullen belegt ist, wird sie mit 0V bezeichnet. In dem Moment, wenn ein Wert in ihr erscheint (sowohl für den Fall, dass dieser Wert dort willkürlich eingetragen wird, wie auch als natürlichen Folge einer Berechnung) wird sie zu 1V. Wird ein Wert durch einen anderen Wert ersetzt, dann wird die Variable zu 2V und so weiter. Wenn ein vorheriger Wert wieder durch Null ersetzt wird, dann wird die Variable wieder zu 0V, auch wenn sie zuvor bereits mit nV bezeichnet war. Wenn danach wiederum ein neuer Wert eingesetzt wird, so wird die Variable nun mit n+1V bezeichnet (wie es auch geschehen wäre, falls sie nicht zwischenzeitlich 0V gewesen wäre) &c. &c. Direkt vor dem Beginn einer Berechnung, nachdem die Daten vorgegeben sind und alles für den Start des Mechanismus eingerichtet und vorbereitet ist, sind die oberen Indizes aller Variablen mit Daten auf Eins gesetzt und die Arbeits- und Ergebnisvariablen sind alle mit Null indiziert. In diesem Zustand präsentiert sie das Diagramm.
Eine Gruppe von Indizes dieser Art hat einige Vorteile, aber diese Vorteile sind wahrscheinlich von der Sorte, die nicht sofort einsichtig sind, falls der Betrachter nicht ein wenig damit vertraut ist, die aufeinander folgenden Schritte zu verfolgen, mit denen die Maschine ihre Aufgaben bearbeitet. Wir haben nur den Platz allgemein darauf hinzuweisen, dass die ganze Notation der Tabellen durch diese Indizes konsistenter wird, weil sie in bestimmten Fällen auf einen Unterschied hinweisen, wo ohne sie eine in der Tendenz verwirrende Identität vorzuliegen schiene. In einem Fall wie Vn=Vp+Vn ergibt sich eine klarere und mit den üblichen Gesetzen der algebraischen Notation konsistentere Darstellung, wenn wir in der Lage sind m+1Vn=qVp+mVn zu schreiben. Es ist ebenso offensichtlich, dass die Indizes eine leistungsfähige Hilfe bei der Zurückverfolgung der Herleitung eines beliebigen Ergebnisses gestatten und ein Wahrnehmen der verschiedensten Umstände, die eine solche Folge von schrittweisen Ersetzungen betreffen, bei denen jedes Ergebnis tatsächlich nur die letzte Konsequenz ist. Solche Umstände könnten in bestimmten Fällen Beziehungen mit einschließen, deren Beobachtung wichtig ist, entweder aus rein analytischen Gründen, oder um bei ihrem Auftreten den Arbeitsvorgang der Maschine passend anzugleichen. Die Abfolgen von Ersetzungen, die zu den Gleichungen des Diagrammes führen, sind wie folgt:—
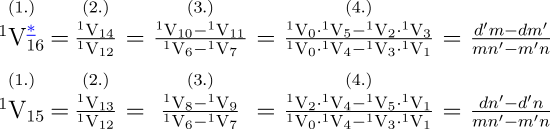
Es gibt für jede dieser Gleichungen drei aufeinander folgende Ersetzungen. Die Gleichungen (2.), (3.) und (4.) sind implizit in (1.) enthalten, wobei wir letztere für einen verdichteten Ausdruck jeder der vorherigen ansehen können. Wir werden sehen, dass jede der aufeinander folgenden Ersetzungen doppelt so viele Vs enthalten muss wie ihr Vorgänger. Wenn in einem Problem n Ersetzungen enthalten sind, dann ist die aufeinander folgende Zahl von insgesamt benötigten Vs 2, 4, 8, … 2n.
Die Ersetzungen in den vorangegangenen Gleichungen sind für die Illustration der Leistungsfähigkeit und Anwendung der oberen Indizes von wenig Wert, da die Indizes in diesem Fall, aufgrund der Natur dieser spezifischen Gleichungen, durchgängig alle mit Eins angegeben sind. Wir wünschten, wir hätten den Raum zur Verfügung, um vollständiger auf solche Relationen einzugehen, die wir in vielen Fällen mit Hilfe dieser Indizes verfolgen könnten.
L. M. Menabrea führt die drei mittleren Spalten seiner Tabelle unter dem allgemeinen Titel Variablenkarten. Die Vs repräsentieren dabei in Wirklichkeit jedoch die Variablenspalten der Maschine und nicht die Karten, die zu diesen gehören. Dennoch ist dieser Titel sehr angemessen, da jede der unter diesem Titel angeführten Relationen durch die spezielle Auswirkung bestimmter Variablenkarten (generell in Kombination mit der Vermittlung durch Operationskarten) bestimmt wird.
Wir nehmen einmal an, dass wir in Erfahrung bringen wollen, wie oft eine bestimmte Größe, oder eine Kombination von Größen, während einer Berechnung in Gebrauch ist. Wir können dies leicht dadurch erfahren, dass wir die vertikale Spalte oder die Spalten des Diagrammes inspizieren, in denen diese Größe auftreten kann. Im aktuellen Fall sehen wir daher, dass all die Daten, wie auch all die Zwischenergebnisse, zwei Mal genutzt werden, mit Ausnahme von (mn' − m'n), welches drei Mal in benötigt wird.
Die Anordnung der Operationen, mit der die Ausführung es aktuellen Beispiels möglich ist, erlaubt es uns alle elf Operationen, aus denen es besteht, mit nur drei Operationskarten zu bewirken, da das Problem von einer Art ist, die es zulässt, dass jede Klasse von Operationen in einer Gruppe zusammen ausgeführt werden können. Alle Multiplikationen, eine nach der anderen, dann alle Subtraktionen, eine nach der anderen, &c. Die Operationen sind {6(×), 3(-), 2(÷)}.
Weil schon die Definition einer Operation impliziert, dass es zwei Zahlen geben muss, mit denen gearbeitet wird, gibt es natürlich für jede Operationen notwendigerweise auch zwei eingebende Variablenkarten, die die zwei passenden Zahlen auswählen (siehe Notiz B). Weiterhin beinhaltet jede Operation, da sie ein Ergebnis produziert, das irgendwo platziert werden muss, eine ausgebende Variablenkarte, die eine passende Stelle für das Ergebnis bezeichnet. Es sind daher bei jeder Berechnung wenigstens drei Mal so viele Variablenkarten in Benutzung, wie es Operationen gibt (nicht Operationskarten, da diese ja, wie wir eben gesehen haben, keineswegs dieselbe Anzahl haben müssen, wie die vorhandenen Operationen ). Tatsächlich ist unter bestimmten Voraussetzungen eine noch größere Menge nötig, wie zum Beispiel in dem Fall, wenn dasselbe Ergebnis in mehr als einer Variable gleichzeitig auftauchen soll (was nicht selten eine Voraussetzung für die später folgenden Aufgaben einer Berechnung ist), sowie auch in weiteren Fällen, auf die wie hier nicht eingehen wollen. Wir sehen daher, dass ein großes Missverhältnis zwischen der Menge an Variablen- und Operations-Karten besteht, die selbst zur Berechnung der einfachsten Aufgaben notwendig sind.
Nicht alle Berechnungen gestatten es, so wie diese, Operationen derselben Art in Gruppen zusammengefasst auszuführen. Wahrscheinlich sind es nur sehr wenige, mit Ausnahmen in der ein oder anderen Stufe des Ablaufs, und einige Berechnungen werden überhaupt keine Zusammenfassungen erlauben. Die Abfolge von Operationen, die in jedem einzelnen Fall ausgeführt werden sollen, ist eine sehr interessante und spannende Frage, die zu behandeln uns der Raum fehlt. In beinahe jeder Berechnung sind viele unterschiedliche Wege für die Ausführung der Prozesse möglich und für die Auswahl der passenden für den Einsatz in einer Rechenmaschine ist verschiedene Überlegungen notwendig. Ein wesentliches Ziel ist es solche Wege auszuwählen, die zur minimalen Ausführungszeit für die Berechnung tendieren.
Es müsste nun klar sein, wie facettenreich und daher kompliziert die Überlegungen sind, die das Betreiben einer solchen Maschine beinhaltet. Es existieren oftmals etliche unterschiedliche Gruppen von Effekte, die gleichzeitig auftreten, die in gewisser Weise voneinander unabhängig sind und dennoch in größerem oder kleinerem Umfang eine gegenseitigen Einfluss aufeinander nehmen. Diese wechselseitigen Einflüsse zu berücksichtigen und sie überhaupt wahrzunehmen und vollständig korrekt im Umfang und mit Erfolg zu verfolgen, birgt Schwierigkeiten in sich, deren Natur bis zu einem gewissen Grad auch Teil jeder Frage sind, die eine große Anzahl an sich gegenseitig komplizierenden Bedingungen enthält, wie zum Beispiel die Voraussage der wechselseitigen Beziehungen bei statistischen Phänomenen, wie auch die in vielen weiteren Faktenklassen auftretenden.
A.A.L.
Das aktuelle Beispiel wurde vor allen Dingen wegen seiner Kürze und Einfachheit gewählt, mit der es einen Blick auf die Art und Weise wirft, in der die Maschine im Falle einer analytischen Berechnung mit Variablen vorgehen würde, weniger um den Umfang ihrer Leistungsfähigkeit zur Lösung von schwierigen und komplexen Fällen zu illustrieren. Die Gleichungen im ersten Beispiel der Denkschrift stellen tatsächlich ein komplizierteres Problem als dieses dar.
Wir haben kein Diagramm zur Entwicklung dieses neuen Beispiels angefügt, wie wir es für das vorherige machten, da es, nach der vollständigen Anwendung dieser Diagramme zur Erläuterung der exzellenten Tabellen von L. M. Menabrea, nun unnötig wäre.
Es wäre anzumerken, dass zwischen der Formel
die in der Denkschrift als Datum zur Berechnung angegeben ist, und den Ergebnissen der Berechnungen, wie sie im letzten Abschnitt der sie begleitenden Tabelle entwickelt sind, eine leichte Diskrepanz besteht. Um mit letzterem völlig übereinzustimmen, hätten die Daten folgendermaßen vorgegeben werden sollen
Das Folgende ist ein komplizierteres Beispiel der Art, in der die Maschine trigonometrische Funktionen mit Variablen berechnen würde. Es ist die Multiplikation von
| A+A1cos |
|
| mit | B + B1cos |
Lassen Sie uns das resultierende Ergebnis in der allgemeinen Form darstellen
| C0 + C1cos |
(1.) |
Diese trigonometrische Reihe ist nicht nur in sich selbst sehr geeignet zur Illustration der Prozesse der Maschine, es ist ebenso sehr von praktischem Interesse wegen seiner häufigen Anwendung in astronomischen Berechnungen. Bevor wir mit ihm fortfahren, sollten wir darauf hinweisen, dass es drei sehr verschiedene Klassen von Wegen gibt, mit denen man gewünschte numerische Werte aus einer analytischen Formel ableiten kann.
Erstens könnten wir uns wünschen, den numerischen Gesamtwert der ganzen Formel zu finden, ohne uns dabei auf die für diese Gleichung als Funktionswerte dienenden Größen zu beziehen, oder auf deren spezielle Kombination und Verteilung, für welche die Formel steht und die sie repräsentiert. Werte dieser Art sind, im engsten Sinne des Begriffes, von strikt arithmetischer Natur, und sie enthalten keinerlei Spur der Vorgänge, durch deren Ablauf sie hergeleitet wurden. Tatsächlich könnte jeder solche numerische Wert aus einer unendlichen Vielfalt von Daten oder Problemstellungen gewonnen worden sein. Die Werte für x und y in den beiden Gleichungen (siehe Notiz D.) fallen in diese Klasse von numerischen Ergebnissen.
Zweitens könnten wir vorschlagen, den zusammengefassten numerischen Wert jedes Terms einer Gleichung oder Serie zu berechnen und diese Ergebnisse separat vor zu halten. Die Maschine muss in diesem Fall entsprechend viele Spalten für Ergebnisse haben, wie es zu berechnende Terme gibt.
Drittens könnte es gewünscht sein, den numerischen Wert von verschiedenen Unterabteilungen jedes Terms zu berechnen und all diese Ergebnisse separat zu führen. Es könnte zum Beispiel vorgegeben sein, dass jeder Koeffizient separat von seiner Variablen berechnet wird, wobei die Maschine in diesem Fall für jeden Term, der sowohl eine Variable, als auch einen Koeffizienten enthält, jeweils zwei Ergebnisspalten zur Verfügung haben muss.
Es gibt viele vorstellbare Wege, auf welche die Verteilung und Abteilung der numerischen Werte in speziellen Fällen einer algebraischen Formel gewünscht sein könnte und es ist eine essenzielle algebraische Eigenschaft der Analytischen Maschine, solche Verteilungen zu jedem gewünschten Grad zu leisten. Viele, oder auch nicht mit mathematischen Studien beschäftigte Personen, könnten nun zu der Auffassung gelangen, dass die Maschine, weil ihre Aufgabe darin liegt Ergebnisse in numerischer Notation anzugeben, bei den Abläufen von Prozessen in ihrem Inneren demnach aritmetisch und numerisch arbeitet, nicht etwa algebraisch und analytisch. Das ist ein Fehler. Die Maschine kann ihre numerischen Größen exakt so arrangieren und kombinieren, als wären sie Buchstaben oder andere allgemeine Symbole und sie könnte ihre Ergebnisse tatsächlich in algebraischer Notation ausgeben, nachdem sie entsprechend vorbereitet würde. Sie könnte drei Sätze von Ergebnissen simultan entwickeln, etwa symbolische Ergebnisse (wie bereits in den Notizen A und B angesprochen), numerische Ergebnisse (ihre vorrangige und hauptsächliche Aufgabe) und algebraische Ergebnisse in wörtlicher Notation. Letzteres wurde jedoch nicht für eine notwendige oder wünschenswerte Erweiterung der Leistungsmerkmale gehalten, teilweise weil die dafür notwendigen Vorrichtungen die Komplexität und das Ausmaß des Mechanismus in einer Weise vergrößert hätten, die in keinem Verhältnis mit den erreichten Vorteilen stünde, da die Hauptaufgabe der Erfindung darin besteht, die uns bereits bekannten allgemeinen Formeln der Analysis, oder die Formeln deren Bildungsvorschriften uns bekannt sind, in eine numerische Sprache zu übersetzen. Es wäre jedoch ein Fehler anzunehmen, dass nur weil die Ergebnisse in der Notation einer stärker eingeschränkten Wissenschaft gegeben werden, die Prozesse deswegen auf die Prozesse dieser Wissenschaft beschränkt wären. Die Aufgabe der Maschine liegt tatsächlich darin, die bestmögliche praktische Effizienz bei der Anwendung von numerischen Interpretationen der höheren Wissenschaft der Analysis zu liefern, wobei sie die Prozesse und Kombinatorik letzterer anwendet.
Lassen Sie uns nun zu der trigonometrischen Serie zurückkehren. Wir sollten dazu die ersten vier Terme des Faktors (A + A1 cos ![]() + &c.) betrachten, da diese genügen, um die Methode zu zeigen. Wir gebe vor, dass wir den numerischen Wert jedes Koeffizienten C0, C1, &c. von (1.) separat erhalten. Die direkte Multiplikation der zwei Faktoren ergibt
+ &c.) betrachten, da diese genügen, um die Methode zu zeigen. Wir gebe vor, dass wir den numerischen Wert jedes Koeffizienten C0, C1, &c. von (1.) separat erhalten. Die direkte Multiplikation der zwei Faktoren ergibt
| (2.) |
und als Ergebnis würde daher dies auf der Maschine zu sehen sein:—
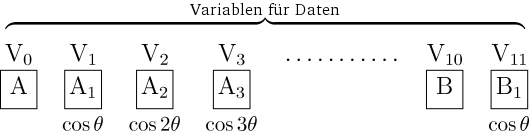

Die zu jedem Koeffizienten gehörende Variable ist unterhalb des Koeffizienten aufgeschrieben, wie wir es bereits in dem Diagramm gemacht haben, das in der Denkschrift beschrieben ist. Die einzige weitere Reduktion, die offenbar auf den ersten Blick in dem vorherigen Ergebnis möglich ist, wäre die Addition von V21 mit V31 (wobei B1A von V31 kopiert würde). Die Operationen insgesamt von Beginn an wären dann—
| Erste Serie von Operationen |
Zweite Serie von Operationen |
Dritte Serie, welche nur eine (letzte) Operation enthält |
| 1V10×1V0 = 1V20 | 1V11×1V0 = 1V31 | 1V21×1V31 = 2V21, und |
| 1V10×1V1 = 1V21 | 1V11×1V1 = 1V32 | V31 wird = 0. |
| 1V10×1V2 = 1V22 | 1V11×1V2 = 1V33 | |
| 1V10×1V3 = 1V23 | 1V11×1V3 = 1V34 |
Wir gehen hier nicht so detailliert auf jeden Schritt des Prozesses ein wie in den Beispielen der Notiz D und G, weil wir dies für unnötig und langatmig halten. Der Leser wird sich an die Bedeutung der oberen und unteren Indices &c. erinnern, die bereits erläutert wurde.
Um fortzufahren: Wir wissen, dass
| (3.) |
Folglich lässt sich, nach ein wenig näherer Betrachtung, die zweite Zeile von (2.) durch passende Substitutionen umwandeln zu
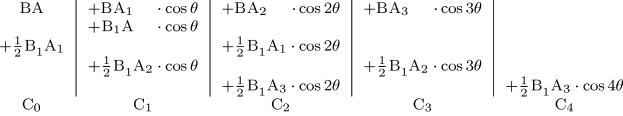
Jeder dieser Koeffizienten sollte in den folgenden Spalten erscheinen
Wenn wir uns die genaue Anordnung der Ergebnisse von (2.) in den Ergebnisspalten ansehen, wie sie im Diagramm dargestellt sind, sehen wir, dass wir, um diese Umwandlung zu bewirken, jeden nachfolgenden Koeffizienten von V32, V33, &c. (beginnend mit V32) mit Hilfe passender Karten durch Zwei dividieren müssen, dass eine der so erhaltenen Hälften zu dem Koeffizienten der Variable addiert werden muss, die zehn Spalten vorher liegt, die andere Hälfte zu dem Koeffizienten der Variablen, die zwölf Spalten zurück liegt. V32, V33, &c. selbst werden während dieses Prozesses auf Null gesetzt.
Diese Serie von Operationen kann folglich ausgedrückt werden als:—
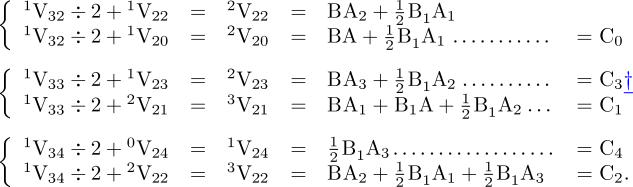
Die Berechnung der Koeffizienten C0, C1, &c. von (1.) wäre damit vollendet und sie wären der Reihe nach in V20, V21, &c. stehen. Man hat dabei festgestellt, dass, beginnend mit der Ausführung der vierten Serie von Operationen, die Variablen V31, V32, &c. sich von Ergebnis-Variablen in einfache Arbeits-Variablen verwandelt haben.
Die Ersetzungen, welche die Maschine während dieser Abläufe für die rechte Seite von (3.) mit der linken Seite durchführt, sind ein exzellentes Beispiel für die Art und Weise, in der wir ihr wahlfrei Aufträge erteilen können, ganz nach Belieben, jede Funktion, jede Zahl oder jeden Prozess für jede beliebige andere Funktion, Zahl oder jeden anderen Prozess zu substituieren, wenn eine bestimmte Bedingung vorliegt.
Wir nehmen nun einmal an, dass wir noch einen Schritt weiter gehen wollen und die numerischen Werte für jeden berechneten Term des Produktes aus (1.) erhalten wollen, also für jeden Koeffizienten zusammen mit seiner Variablen, also ![]() für den (n+1)ten Term.
für den (n+1)ten Term.
Zu diesem Zweck müssen wir die Variablen selbst in einen weiteren Satz von Spalten, V41, V42, &c., platzieren und dann nacheinander ihre Multiplikation mit jeweils V21, V22, &c. ordern. Es gäbe sodann eine letzte Serie von Operationen wie folgt:—
| Fünfte und letzte Serie von Operationen |
| 2V20 × 0V40 = 1V40 |
| 3V21 × 0V41 = 1V41 |
| 3V22 × 0V42 = 1V42 |
| 2V23 × 0V43 = 1V43 |
| 1V24 × 0V44 = 1V44 |
(Anmerkung: die Spalte V40, die den Koeffizienten von V20 enthalten so, der keine Variable hat, wird, als Vorbereitung vor der Ausführung dieser fünften Serie von Operationen, lediglich cos 0![]() (=1) enthalten.)
(=1) enthalten.)
Von dem Moment an, in dem die fünfte und letzte Serie von Operationen angefordert wird, wandeln sich die Variablen V20, V21, &c. von Ergebnis-Variablen in Arbeits-Variablen. V40, V41, &c. sind nun die Empfänger der endgültigen Ergebnisse.
Wir sollten sehen, dass die Variablen cos![]() , cos 2
, cos 2![]() , cos 3
, cos 3![]() , &c., wenn sie ausgefüllt sind, direkt auf V41, V42, &c. angewandt werden, wie es für andere Datenwerte erfolgen würde. Im anderen Fall könnte eine eigene Berechnung in einem separaten Teil der Maschine durchgeführt werden um sie zu berechnen und sie dann in V41, &c. einzutragen.
, &c., wenn sie ausgefüllt sind, direkt auf V41, V42, &c. angewandt werden, wie es für andere Datenwerte erfolgen würde. Im anderen Fall könnte eine eigene Berechnung in einem separaten Teil der Maschine durchgeführt werden um sie zu berechnen und sie dann in V41, &c. einzutragen.
Wir haben somit ausgeführt, wie die Maschine Gleichung (1.) in direkter Art berechnen könnte und zwar unter der Annahme, dass wir nichts über die allgemeinen Terme der sich ergebenden Serie wüssten. Die Maschine würde jedoch in der Praxis ganz anders eingestellt, wenn wir (wie in diesem Fall) wissen, wie das Gesetz zur Bildung der allgemeinen Terme aussieht.
Die ersten beiden Terme von (1.) sind
| (4.) |
und die Verallgemeinerung für alle nachfolgenden Terme ist
| (5.) |
was den Koeffizienten für den (n+1)th Term darstellt. Die Maschine würde die ersten beiden Terme durch einen Satz passender Operations-Karten berechnen und würde dann einen anderen Satz für den dritten Term benötigen. Dieser letztere Satz von Operations-Karten würde all die nachfolgenden Terme bis ins Unendliche berechnen und dabei lediglich bestimmte neue Variablen-Karten für jeden Term benötigen, damit die Operationen auf die passenden Spalten angewandt werden. Die folgende Abfolge von Operationen wäre nötig, um die Koeffizienten der Terme für n+2 zu berechnen:—
Wir könnten sie auch wie folgt darstellen, in der numerischen Reihenfolge der Operationen:—
Es sollte klar sein, dass die Klammern die Beziehungen zwischen den Operationen darstellen, in denen sie gruppiert werden können, während ein Komma die Abfolge darstellt. Das Symbol + könnte für letztere Darstellung genutzt werden, jedoch könnte dies leicht zu Verwirrungen führen, da + notwendigerweise auch zur Bezeichnung einer der ausgeführten Operationen innerhalb dieser Abfolgen genutzt wird. In Übereinstimmung mit dieser dem Komma zugedachten Bedeutung muss sorgfältig mit dem Fall umgegangen werden, wenn eine Gruppe von Operationen mehr als einmal wiederholt wird, wie das in obigem Fall bei n(11…15) geschieht. Dort steht kein Komma nach der Zahl oder dem Buchstaben, die dieser Gruppe vorausgehen. n, (11…15) stünde für eine Operation n, gefolgt von einer Gruppe von Operationen (11…15), statt die Anzahl der aufeinander folgenden Gruppen zu bezeichnen.
Immer dann, wenn ein allgemeines Glied existiert, wie in obigem Beispiel, wird es auch eine sich wiederholende Gruppe von Operationen geben. Sowohl wegen der Kürze, als auch zur besseren Unterscheidung, bezeichnen wir eine sich wiederholende Gruppe kurz als Zyklus. Ein Zyklus von Operationen ist dann als ein beliebiger Satz von Operationen zu verstehen, der mehr als einmal wiederholt wird. Ein Zyklus kann dabei aus einem nur zweimaligen Durchlauf bestehen oder auch aus einer unbestimmten Anzahl von Wiederholungen, da der Fakt einer überhaupt auftretenden Wiederholung schon einen Zyklus ausmacht. In vielen Fällen der Analysis gibt es eine wiederholte Gruppe von einem oder mehreren Zyklen, also den Zyklus eines Zyklus oder auch einen Zyklus von Zyklen. Nehmen wir zum Beispiel an, wir wollten eine Serie durch eine andere Serie teilen,
| (1.) |
wobei gefordert sein soll, dass das Ergebnis, etwa Dividend und Divisor, in aufsteigenden Potenzen von x entwickelt werden soll. Ein kurzes Zurückdenken an (1.) und an die bei einer algebraischen Division notwendigen Schritte zeigt uns, dass (wenn wir annehmen, dass der Nenner aus p Termen besteht) der erste partielle Quotient durch folgende Operationen aufgelöst wird:—
| (2.) | {(÷), p(×, −)} or {(1), p(2, 3)}, |
Der zweite partielle Quotient wird durch einen ganz ähnlichen Satz von Operationen aufgelöst, der auf den Rest des im ersten Satz erhaltenen Ergebnisses angewandt wird, statt auf den ursprünglichen Dividenden. Alle Prozesse, die bis zum Zeitpunkt der Bestimmung des zweiten partiellen Quotienten durchlaufen wurden, wären daher—
| (3.) | 2{(÷), p( × , −)} or 2{(1), p(2, 3)}, |
wobei es sich um einen Zyklus handelt, der einen Zyklus enthält, oder einen Zyklus zweiter Ordnung. Die Operationen für die vollständige Division, bei der wir annehmen, dass n Terme der Serie den Quotienten ausmachen, wären dann—
| (4.) | n{(÷), p( × , −)} or n{(1), p(2, 3)}, |
Man muss natürlich daran denken, dass der Prozess der algebraischen Division in Wirklichkeit bis zum Unendlichen fortgeführt wird, ausser in den wenigen Fällen, in denen wir einen exakten Quotienten erhalten können. Die Zahl n in Formel (4.) ist immer eine selbst gewählte Anzahl und der nte partielle Quotient ist der Koeffizient der (n-1)ten Potenz von x.
Es gibt einige Fälle, in denen Zyklen von Zyklen von Zyklen in einer unbestimmten Anzahl vorkommen. Solche Fälle sind normalerweise sehr kompliziert und sie sind im Rahmen der Maschine extrem interessant. Die algebraische Entwicklung in eine Serie der nten Funktion einer beliebigen gegebenen Funktion ist von dieser Sorte. Lassen Sie uns annehmen, wir möchten die nte Funktion von
| (5.) |
Wir sollten voraus schicken, dass wir annehmen, der Leser versteht was mit der nten Funktion gemeint ist. Genauso nehmen wir an, dass er den Unterschied darin versteht, eine nte Funktion algebraisch zu entwickeln, im Gegensatz zu einer Berechnung der nten arithmetischen Funktion. Wenn dies nicht der Fall ist, dann wird das Folgende in keiner Weise besonders verständlich sein, aber wir haben nicht ausreichend Platz, um auch nur beiläufige Erklärungen zu geben. Um fortzufahren: das Gesetz, nach dem die folgenden Funktionen von (5.) zu entwickeln sind, muss natürlich zunächst festgelegt werden. Dieses Gesetz kann eines von vielen verschiedenen sein. Wir können vorgeben, dass wir unsere Ergebnisse in aufsteigenden Potenzen von x wünschen, wobei die allgemeine Form dann folgendermaßen aussähe
oder, in aufsteigenden Potenzen von n selbst, dem Index der Funktion, die wir am Ende erhalten. Dann sähe die allgemeine Form folgendermaßen aus
und x würde nur in die Koeffizienten eingehen. Es können wiederum auch andere Funktionen als Potenzen von x oder von n ausgewählt werden. Zusätzlich könnte man vorgeben, dass die Koeffizienten selbst nach vorgegebenen Funktionen aus einer bestimmten Menge arrangiert werden. Ein weiterer Modus wäre, die Gleichungen nach ihren Koeffizienten anzuordnen, wobei unter den verschiedenen Funktionen dann durch gemeinsame Betrachtung dieser Gleichungen und von (5.) selbst bestimmt werden müsste, bei welcher von ihnen eine Entwicklung der nten Funktion von (5.) möglich ist.
Die algebraische Natur der Maschine (auf der wir im vorherigen Teil dieser Notiz so stark bestanden haben) würde es ihr ermöglichen, jeden dieser verschiedenen Wege zu beschreiten. Wie wir ja kurz zuvor gezeigt hatten, kann sie die numerischen Ergebnisse jeglicher vorgegebenen Serie von Prozessen in perfekter Weise nach Bedarf verteilen und separieren. Wäre dies anders, könnte die Maschine lediglich die arithmetische nte Funktion berechnen - ein Ergebnis, das wie jedes andere rein arithmetische Ergebnis am Ende einfach eine Zahl wäre, bar jeglicher Spur der Daten oder Prozesse, die zu ihr geführt haben.
Zweitens wäre, nachdem das Gesetz zur Bildung der nten Funktion ausgewählt ist, der nächste Schritt offensichtlich die Entwicklung von (5.) selbst nach diesem Gesetz. Dieses Ergebnis wäre die erste Funktion und man würde sie durch eine bestimme Serie von Prozessen erhalten. Diese Prozesse enthielten in den meisten Fällen einen oder mehrere Zyklen von Operationen.
Der dritte Schritt (der aus den verschiedenen notwendigen Prozessen für die anstehende Ersetzung der Variablen selbst durch die Serie, welche die erste Funktion ausmacht, bestünde) könnte einen von zwei Wegen beschreiten: die Ersetzung könnte entweder für jedes x in der ursprünglichen Gleichung (5.) erfolgen, oder, ganz ähnlich, für jedes in der ersten Funktion selbst erscheinende x, wobei diese erste Funktion äquivalent zu (5.) ist. In einigen Fällen könnte der erste Weg der bessere sein, in anderen Fällen letzterer.
Welcher Weg auch immer gewählt wird, es muss klar sein, dass das Ergebnis als eine nach dem für die Entwicklung der nten Funktion vorgegebenen Gesetz angeordnete Serie erscheint. Dieses Ergebnis macht die zweite Funktion aus, mit der wir exakt so fortfahren, wie mit der ersten Funktion, um sodann die dritte Funktion zu erhalten und so weiter, insgesamt n-1 Mal, um endlich die nte Funktion zu erhalten. Wir sehen leicht ein, dass, weil jede nachfolgende Funktion als demselben Gesetz folgende Serie angeordnet ist, wir es hier (nachdem die erste Funktion bestimmt ist) mit einem Zyklus in einem Zyklus in einem Zyklus &c. von Operationen zu tun haben, eins, zwei, drei, bis hinauf zu n-1 Mal, zur Berechnung der nten Funktion. Wir sagen nachdem wir die erste Funktion erhalten haben, weil für die erste Funktion (aus Gründen, auf die wir hier nicht eingehen können) in vielen Fällen eine Entwicklung nach einem besonderen Satz von Prozessen erfolgt, der für die restlichen Funktionen nicht wiederholt wird.
Wir haben nun nichts als einen oberflächlichen Blick auf die prinzipiellen allgemeinen Schritte geworfen, die notwendig wären, um die nte Funktion einer solchen Formel wie (5.) zu erhalten. Die Fragestellung ist so außerordentlich kompliziert, dass, wie wahrscheinlich zu erwarten ist, nur wenige Personen ihr zur eigenen Zufriedenheit folgen können, da wir hier auf so kurze und allgemeine Aussagen über dieses Thema beschränkt sind. Es handelt sich dennoch um einen wichtigen Fall im Rahmen der Maschine und gibt eine Vorstellung von besonderer Art, die wir nicht einfach ohne wenigstens eine Andeutung übergehen wollten. Nichts könnte interessanter sein, als der Lösung eines solchen, wie des oben erwähnten, Falles durch die Maschine in jedem Detail zu folgen, aber die Zeit, der Platz und die Arbeit, die dies erforderte, würde nur in den Rahmen einer sehr ausführlichen Arbeit passen.
Um zum Thema der Zyklen von Operationen zurückzukehren: einiges in der Notation der Integralrechnung führt selbst sehr treffend dorthin. Gleichung (2.) könnte deshalb auch wie folgt angegeben werden—
| (6.) |
wobei p für die Variable steht, (+ 1)p für die Funktion der Variablen, also für ![]() p in den Grenzen von 1 bis p, oder von 0 bis p-1, mit einer Schrittweite von 1. Dementsprechend könnte man (4.) wie folgt schreiben—
p in den Grenzen von 1 bis p, oder von 0 bis p-1, mit einer Schrittweite von 1. Dementsprechend könnte man (4.) wie folgt schreiben—
| (7.) |
mit n in den Grenzen von 1 bis n oder von 0 bis n-1,
| (8.) | oder |
Man mag vielleicht denken, dass diese Notation lediglich ein umschreibender Weg ist um das darzustellen, was einfacher und genau so effektiv bereits zuvor ausgedrückt wurde und in obigem Beispiel mag dies bis zu einem gewissen Grad zutreffen. Es gibt jedoch eine weitere Beschreibung von Zyklen, die nur in einer solch zusammenfassenden Form ausgedrückt werden kann, wie sie die vorangehende Notation bietet. Wir wollen diese Art von Zyklen als variierende Zyklen bezeichnen. Sie treten häufig auf und bestehen aus aufeinander folgenden Zyklen von Operationen der folgenden Art:—
| (9.) |
wobei jeder Zyklus dieselbe Gruppe von Operationen beinhaltet, jedoch die Anzahl der Wiederholungen einer Gruppe mit einer festen Rate in jedem Zyklus variiert. (9.) kann gut wie folgt ausgedrückt werden:—
| (10.) |
Unabhängig von den dieser Notation aus der Integralrechnung innewohnenden Vorteile, die wir nun in bestimmten Fällen anerkennen, gibt es auch Überlegungen, die sie wegen ihrer Verbindungen und Beziehungen innerhalb dieses neuen Anwendungsfalles interessant machen. Es war in einigen der vorherigen Notizen zu erkennen, dass die in der Analysis genutzten Prozesse ein logisches System von wesentlich mehr Allgemeingültigkeit liefern, als allein ihre Anwendung auf Zahlen. Wenn wir also eine beliebige algebraische Formel sehen, sie dabei ausschließlich mit Bezug auf die Prozesse der Maschine betrachten und für den Moment ihre abstrakte Bedeutung in Mengenbeziehungen beiseite lassen, dann repräsentieren die Symbole +, ×, &c. tatsächlich (als ihre direkte und nächste Auswirkung, wenn die Formel auf die Maschine angewandt wird), dass ein bestimmtes Prisma, welches einen Teil des Mechanismus ausmacht (siehe Notiz C), eine neue Seite vorzeigt und so eine neue Karte präsentiert, die wiederum auf die Bündel von Hebeln der Maschine einwirkt. Diese neue Karte ist mit den jeweils passend arrangierten Löchern perforiert, welche für die Operationen der Addition, der Multiplikation, &c. notwendig sind. Auch in diesem Fall repräsentieren die Zahlen der vorhergehenden Formel (8.) in der Praxis jeweils eine dieser Karten, die über das Prisma aufgehängt sind.
Diese Anwendung der Notation aus der Integralrechnung, wie wir sie in den Formeln (7.), (8.) und (10.) gesehen haben, hat uns einen kurzen Ausblick auf ähnliche neue Anwendungsmöglichkeiten der Sprache der höheren Mathematik gewährt. ![]() steht hier in der realen Anwendung dafür, dass, wenn eine bestimmte Anzahl von Karten nacheinander abgearbeitet wurde, das Prisma, über das sie laufen, nun zurück rotieren muss, bis die Karten wieder in ihrer Ausgangsposition sind. Die Grenzen 1 bis n, 1 bis p &c. legen dabei fest, wie oft diese Rückwärts-Rotation wiederholt werden muss.
steht hier in der realen Anwendung dafür, dass, wenn eine bestimmte Anzahl von Karten nacheinander abgearbeitet wurde, das Prisma, über das sie laufen, nun zurück rotieren muss, bis die Karten wieder in ihrer Ausgangsposition sind. Die Grenzen 1 bis n, 1 bis p &c. legen dabei fest, wie oft diese Rückwärts-Rotation wiederholt werden muss.
A.A.L.
Es existiert ein wunderschön gewobenes Portrait von Jacquard, zu dessen Herstellung 24.000 Karten benötigt wurden.
Die Leistungssteigerung durch das Wiederholen von Karten, auf das L. M. Menabrea eingeht und das ausführlicher in Notiz C erklärt wird, reduziert die Anzahl der benötigten Karten immens. Es ist offensichtlich, dass diese mechanische Verbesserung speziell dann anwendbar ist, wenn Zyklen in den mathematischen Operationen auftauchen und dass, wenn Daten für Berechnungen durch die Maschine vorbereitet werden, man die Reihenfolge und Kombination der Prozesse mit einem Blick darauf auslegen sollte, sie so oft wie möglich symmetrisch und zyklisch zu machen, damit die mechanischen Vorteile des Vorratsspeichers maximal ausgenutzt werden können. Hier ist es interessant, die Art und Weise zu beobachten, in welcher der Wert einer analytischen Quelle durch einen genialen mechanischen Beitrag erreicht und verbessert wird. Wir sehen hier einen Fall von gegenseitigen Anpassungen zwischen den rein mathematischen und den mechanischen Abteilungen, die bereits in Notiz A als eine hauptsächliche und essenzielle Vorbedingung für den Erfolg der Erfindung einer Rechenmaschine erwähnt wurden. Die Natur der durch solche Anpassungen gewonnen Ressourcen wäre von einer von zwei prinzipiellen Arten. In einigen Fällen würde eine Schwierigkeit (die vielleicht in sich selbst unlösbar wäre) der einen Abteilung durch die Möglichkeiten der anderen überwunden. In anderen Fällen (wie dem gegenwärtigen) würde eine bestimmte Stärke in einem Punkt der einen Abteilung für den zugehörigen Punkt der anderen Abteilung noch weiter verstärkt und noch besser verfügbar gemacht.
Lediglich als Beispiel für den Grad, in dem die kombinierten Systeme von Zyklen und Vorratsspeicher die Anzahl der benötigten Karten schrumpfen können, wählen wir einen Fall, in dem diese Eigenschaften sich deutlich zeigen und der zugleich den Vorteil hat, von einer ganz anderen Art von Problem zu handeln, als die in den sonstigen Notizen irgendwo erwähnten. Nehmen wir an, wir wollten neun Variablen aus zehn einfachen Gleichungen folgender Form eliminieren—
| ax0 + bx1 + cx2 + dx3 + ··· | = p | (1.) |
| a1x0 + b1x1 + c1x2 + d1x3 + ··· | = p' | (2.) |
| &c. &c. &c. | &c. |
Bevor wir fortfahren sollten wir erklären, dass es uns bei diesem Problem nicht darum geht, die tatsächliche Anordnung der Daten auf den Variablen Maschine zu durchdenken, sondern es vielmehr als eine abstrakte Frage nach der Natur und der Anzahl der Operationen zu sehen, die während seiner vollständigen Lösung durchgeführt werden.
Im ersten Schritt stünde die Elimination der ersten unbekannten Größe x0 zwischen den ersten beiden Gleichungen. Diese würde in folgender Form erreicht—
wobei die Operationen 10 (×, ×, −) benötigt würden. Der zweite Schritt wäre die Elimination von x0 zwischen der zweiten und dritten Gleichung, wobei die Operationen exakt dieselben wären. Wir sollten dann alle die folgenden Operationen durchgeführt haben:—
In derselben Weise fortfahrend, wäre die Gesamtzahl der Operationen für die vollständige Eliminierung von x0 zwischen allen aufeinander folgenden Paaren von Gleichungen—
Danach sollten wir nun neun einfache Gleichungen von neun Variablen haben, aus denen wir die nächste Variable x1 eliminieren wollen und die Gesamtzahl der Prozesse wäre
Wiederum danach hätten wir noch acht einfache Gleichungen mit acht Variablen, aus denen wir x2 eliminieren wollen. Die Gesamtzahl dieser Prozesse wäre—
und so weiter. Die Gesamtanzahl der Operationen für die Eliminierung aller Variablen wäre daher—
Es würden hier drei Operations-Karten die Aufgabe von 330 solcher Karten erfüllen.
Wenn wir n einfache Gleichungen mit n−1 Variablen annehmen, wobei n eine Zahl mit unbeschränkter Größe ist, wird dieser Fall noch deutlicher, weil dieselben drei Karten dann die Stelle von Tausenden oder Millionen von Karten einnehmen könnten.
Wir möchten weiterhin die Aufmerksamkeit auf die bereits angemerkte Tatsache lenken, dass es keineswegs notwendig ist, die für eine Lösung vorgeschlagene Formel als Voraussetzung dafür, dass die Maschine in der Lage ist sie zu lösen, je tatsächlich ausgearbeitet zu haben. Wenn wir nur die Serie von Operationen kennen, die durchlaufen werden müssen, dann ist dies bereits ausreichend. Im vorangegangenen Beispiel wird dies durch eine kurze Überlegung offensichtlich genug. Und dieser Umstand verdient eine besondere Erwähnung, da hierin vielleicht ein latenter Wert einer solchen Maschine liegt, dessen Bedeutung im Gesamtergebnis nicht leicht zu berechnen wäre. Wir wissen bereits, dass es Funktionen gibt, deren numerischer Wert sowohl für die abstrakte, wie auch für die praktische Wissenschaft, sehr wichtig ist, wobei die Bestimmung eines solchen Wertes aber so langwierige und komplizierte Prozesse benötigt, dass sie, obwohl sie durch den Einsatz von sehr viel Zeit, Arbeit und Geld erreichbar wären, in diesen Fällen bis jetzt als praktisch nicht erreichbar gelten. Und wir verstehen auch, dass es einige Ergebnisse gibt, die in der Praxis mit auch nur irgendeiner Genauigkeit zu erreichen absolut unmöglich ist, deren exakte Bestimmung aber für die zukünftigen Bedürfnisse der Wissenschaften mit ihren vielfältigen, komplizierten und sich schnell fort entwickelnden Forschungsfeldern, sehr wichtig sein könnte.
Ohne nun in den Bereich der Behauptungen gehen zu wollen, möchten wir dennoch ein spezielles Problem erwähnen, dass uns in diesem Moment als ein passendes Beispiel für den Nutzen einer solchen Maschine erscheint, die solche Dinge ermitteln kann, deren Ausarbeitung für menschliche Gehirne schwierig oder unmöglich wäre. Bei der Lösung des berühmten Drei-Körper-Problems gibt es unter den ungefähr 295 von M. Clausen (Astroe. Nachrichten, No. 406) angegebenen Koeffizienten der lunaren Störungen als Ergebnis der Berechnungen von Burg, zweier von Damoiseau und einer von Burckhardt, vierzehn Koeffizienten, die sich in der Art ihrer algebraischen Vorzeichen unterscheiden. Unter den verbleibenden sind nur 101 (oder ungefähr ein Drittel) die präzise sowohl in ihren Vorzeichen, wie auch ihrem Wert übereinstimmen. Diese Unstimmigkeiten, die im allgemeinen individuell nur eine sehr kleine Größe haben, können entweder durch eine fehlerhafte Bestimmung der abstrakten Koeffizienten bei der Entwicklung des Problems entstanden sein, durch Unterschiede in den aus Beobachtungen hergeleiteten Daten, oder durch eine Kombination beider Ursachen. Das Vorangegangene ist die häufigste Quelle von Fehlern in astronomischen Berechnungen und diese Maschine würde sie vollständig vermeiden.
Wir könnten sogar Gesetze für Serien oder Formeln in beliebiger Art entwickeln und die Maschine darauf ansetzen, diese auszuarbeiten und so numerische Ergebnisse herzuleiten, an die zu suchen wir sonst nie gedacht hätten. Doch wäre dies wohl kaum jemals von irgendeiner praktischen Nützlichkeit, noch würde dem höherer Wert beigemessen, als einer philosophischen Spielerei.
A.A.L.
Es ist wünschenswert, möglicherweise übersteigerte Vorstellungen im Bezug auf die Leistungsfähigkeit der Analytischen Maschine abzuwehren. Bei der Betrachtung eines neuen Themas tritt, zunächst, häufig eine Tendenz dazu auf, das bereits interessante oder erwähnenswerte zu überbewerten und zweitens, bedingt durch eine Art natürlicher Reaktion, den wahren Status eines Falles unterzubewerten wenn wir entdecken, dass unsere Erwartungen über das haltbare Maß hinausgingen.
Die Analytische Maschine erhebt keinerlei Anspruch darauf, irgendetwas ins Leben zu rufen. Sie kann ausführen, was immer wir ihr an Aufgaben vorgeben können. Sie kann der Analysis folgen, aber sie hat nicht die Fähigkeit, irgendeine analytische Beziehung oder Wahrheit vorauszuahnen. Ihre Fähigkeiten liegen darin, uns Dinge verfügbar zu machen, mit denen wir bereits vertraut sind. Sie ist darauf ausgelegt, dies vor allem und hauptsächlich durch ihre ausführenden Eigenschaften zu bewirken, aber ein indirekter rückwärtiger Einfluss auf die Wissenschaft selbst in anderer Art ist ebenso wahrscheinlich. Dies liegt daran, dass durch die Umverteilung und Kombination der Wahrheiten und Formeln der Analysis, die für den schnellen und einfachen Zugang zur mechanischen Kombinatorik der Maschine erfolgen, die Beziehungen und die Natur vieler Themen in dieser Wissenschaft in ein neues Licht gestellt und grundlegender untersucht werden. Dies ist eine entschieden indirekte und ein wenig spekulative Konsequenz einer solchen Erfindung. Es ist jedoch wegen allgemein gültiger Prinzipien ziemlich offensichtlich, dass bei der Herleitung von mathematischen Wahrheiten in eine neue Form, in die sie für die praktische Anwendung geschrieben und umgesetzt werden müssen, auch neue Einsichten entstehen, die wiederum auf die mehr theoretische Phase eines Themas eine Rückwirkung haben. Es gibt bei allen Erweiterungen der menschlichen Fähigkeiten oder bei Neuerungen im Rahmen des menschlichen Wissens verschiedene kolaterale Einflüsse, die neben den hauptsächlichen und vordergründigen Zielen entstehen.
Um zu den ausführenden Eigenschaften dieser Maschine zurückzukehren: hier sollte bei jedem Mitdenkenden die Frage aufkommenden, ob diese Eigenschaften wirklich in der Lage sind der Analysis in ihrem ganzen Umfang zu folgen? Es kann auf diese Frage keine für jeden befriedigende Antwort gegeben werden, da sie nicht tatsächlich schon existiert und daher keine Erfahrung mit ihren praktischen Ergebnissen vorliegt. Wir wollen aber zur weiteren Betrachtung jedes Lesers die Hauptelemente aufzählen, mit denen die Maschine arbeitet:—
Das Thema Integration und Differenziation verlangt einige Aufmerksamkeit. Die Maschine kann diese Prozesse auf einem von zwei Wegen erreichen:—
Erstens könnten wir mit Hilfe der Operations- und Variablen-Karten von der Maschine fordern, dass sie die verschiedenen Schritte durchläuft, die zur Bestimmung des Grenzwertes einer beliebigen betrachteten Funktion notwendig wären.
Zweitens könnte sie (wenn wir die Form des Grenzwertes für die fragliche Funktion kennen) die Integration oder Differenziation durch Substitution bewirken. Wir haben in Notiz B angemerkt, dass jeder Satz von Spalten mit eingeschriebenen Zahlen lediglich eine allgemeine Funktion dieser Größen repräsentiert, solange, bis die spezielle Funktion mittels der Operations- und Variablen-Karten festgeschrieben wird. Wenn wir folglich statt des Wertes einer Funktion den Wert ihres Integrals anfordern, oder den ihres Differentialkoeffizienten, müssen wir lediglich die jeweilige Kombination der zugehörigen Größen, die dieses Integral oder den Koeffizienten ausmachen, anfordern. Bei axn zum Beispiel, würde statt der Anforderung für die Größen
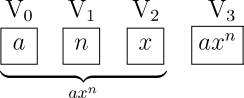
in der Spalte V3 die Kombination axn zu zeigen, stattdessen gefordert, dort
erscheinen zu lassen. Die Spalten sähen also stattdessen wie folgt aus:—
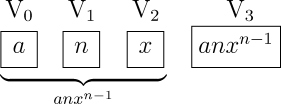
Ganz ähnlich könnten wir auch ![]() , also das Integral von axn, anfordern.
, also das Integral von axn, anfordern.
Ein interessantes Beispiel für die Ablaufverfolgung der Prozesse in der Maschine böte eine Formel wie
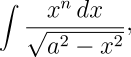
oder jeder andere Fall von Integration durch sukzessive Reduktion, bei der ein Integral, das eine n Mal wiederholte Operation enthält, abhängig von einem weiteren gemacht werden kann, das dieselbe Operation n-1 oder n-2 Mal enthält usw., bis wir durch wiederholte Reduktion eine endgültige Form erreichen, deren Wert dann zu bestimmen ist.
Die Methoden in Arbogasts Calcul des Dérivations sind speziell geeignet für die Notation und Prozesse der Maschine. Ähnlich geeignet ist die Gesamtheit der kombinatorischen Analysis, die zunächst aus rein numerischen Berechnungen von Indizes besteht und im zweiten Schritt in der Verteilung und Kombination der Größen, die bestimmten, an diese Indizes gebundenen Regeln folgt.
Wir wollen diese Notizen mit der detaillierten Verfolgung der Schritte beenden, mittels derer die Maschine die Bernoulli-Zahlen berechnen könnte. Dies ist (in der Form, in der wir es herleiten wollen) ein recht kompliziertes Beispiel für die Möglichkeiten der Maschine. Die einfachste Methode zur Berechnung dieser Zahlen wäre durch die direkte Erweiterung folgender Gleichung möglich
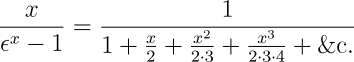 |
(1.) |
welche tatsächlich ein spezieller Fall der Entwicklung von
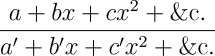
ist, die in Notiz E erwähnt wird. Wir könnten auch von folgender wohl bekannter Form ausgehen
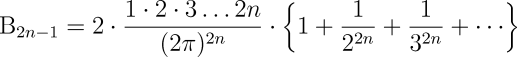 |
(2.) |
oder von dieser
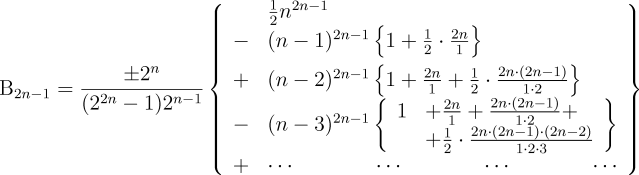 |
(3.) |
oder von einer von vielen weiteren. Da es uns aber nicht um die Einfachheit oder Ermöglichung der Berechnung geht, sonder darum, die Leistungsfähigkeit der Maschine zu illustrieren, bevorzugen wir die unten mit (8.) bezeichnet Formel als Auswahl. Sie wird in der folgenden Weise hergeleitet:—
Wenn wir in der Gleichung
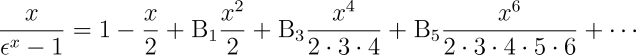 |
(4.) |
(in welcher B1, B3…, &c. die Bernoulli-Zahlen sind) den Nenner auf der linken Seite mit Potenzen von x erweitern und dann Zähler und Nenner durch x dividieren, dann können wir folgende Form herleiten
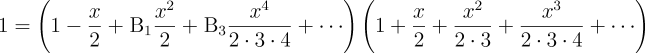 |
(5.) |
Wenn letztere Multiplikation nun ausgeführt wird, erhalten wir eine Serie in der allgemeinen Form
| (6.) |
in der wir zunächst feststellen, dass alle Koeffizienten der Potenzen von x für sich gleich Null sind und zweitens, dass die allgemeine Form für D2n, den Koeffizienten des 2n+1ten Terms (also den von x2n bei geraden Potenzen von x) folgende ist:—
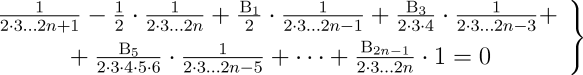 |
(7.) |
Wenn wir jeden Term mit (2·3…2n) multiplizieren, erhalten wir
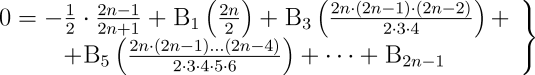 |
(8.) |
was sich auch bequemer in folgender allgemeiner Form schreiben lässt:—
| (9.) |
A1, A3, &c. sind diejenigen Funktionen von n, die jeweils zu B1, B3, &c. gehören.
Wir hätten eine zu (8.) sehr ähnliche Form aus D2n-1 herleiten können , also aus den Koeffizienten jeder ungeraden Potenz von x in (6.), aber diese allgemeine Form weicht ein wenig von den Koeffizienten der ungeraden Potenzen ab und ist nicht ganz so bequem.
Wenn wir (7.) und (8.) näher betrachten, dann sehen wir, dass, wenn diese Formeln, nachdem sie hergeleitet und nur für sich selbst und unabhängig betrachtet werden, von (6.) isoliert stehen, für n auch jede beliebige ganze Zahl gewählt werden könnte, obwohl es offensichtlich ist, dass, falls (7.) als eines der Ds in (6.) auftaucht, n nicht wahlfrei ist, sondern immer eine bestimmte Funktion der Distanz dieses D vom Anfangswert beschreibt. Wenn diese Distanz gleich d ist, dann ist
Wir haben es also nun mit der unabhängigen Gleichung (8.) zu tun, weshalb wir uns daran erinnern müssen, dass die Bedingungen für den Wert von n nun modifiziert sind und dass n eine vollkommen frei wählbare ganze Zahl ist. Dieser Umstand, in Kombination mit dem Fakt (den wir leicht einsehen), dass wie immer n auch gewählt wird, jeder Term von (8.) nach dem (n+1)ten gleich 0 ist und dass der (n+1)te Term selbst immer ![]() ist, erlaubt es uns, den Wert (entweder den numerischen oder den algebraischen) jeder Bernoulli-Zahl B2n-1 in einem Ausdruck mit allen vorherigen zu bestimmen, wenn wir lediglich die Werte für B1, B3…B2n-3 kennen. Wir fügen an diese Notiz ein Diagramm und eine Tabelle an, welche die Details der Berechnung für B7 enthalten (wobei B1, B3, B5 als vorgegeben angenommen werden).
ist, erlaubt es uns, den Wert (entweder den numerischen oder den algebraischen) jeder Bernoulli-Zahl B2n-1 in einem Ausdruck mit allen vorherigen zu bestimmen, wenn wir lediglich die Werte für B1, B3…B2n-3 kennen. Wir fügen an diese Notiz ein Diagramm und eine Tabelle an, welche die Details der Berechnung für B7 enthalten (wobei B1, B3, B5 als vorgegeben angenommen werden).
Wenn wir (8.) eingehend betrachten sehen wir bald, dass wir den numerischen Wert jeder Bernoulli-Zahl in Folge erhalten können, von der allerersten ad infinitum. Dazu führen wir folgende Serie von Berechnungen durch:—
1. Serie.—Wir setzen n=1 und berechnen (8.) für diesen Wert von n. Das Ergebnis ist B1.
2. Serie.—Wir setzen n=2. Bei der Berechnung von (8.) für diesen Wert von n setzen wir den gerade erhaltenen Wert von B1 ein. Das Ergebnis ist B3.
3. Serie.—Wir setzen n=3. Bei der Berechnung von (8.) für diesen Wert von n setzen wir die Werte von B1 und B3 ein, die wir zuvor erhalten haben. Das Ergebnis ist B5. Und so weiter, so oft wir es wünschen.
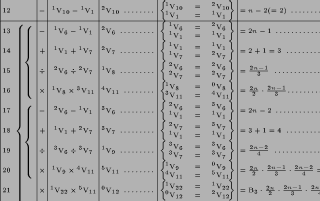
|
|
Das Diagramm der Berechnung der Bernoulli-Zahlen ist sehr groß und kompliziert. Es kann nicht als eingebettetes Bild in diesem Dokument dargestellt werden. Wenn es auf die Größe eine typischen Computer-Bildschirms verkleinert wird, wird der Text im Diagramm unlesbar. Das Diagramm ist in zwei verschiedenen Auflösungen verfügbar. Die folgenden Links zeigen die ausgewählte Version ein einem eigenen Browserfenster (falls Ihr Browser das unterstützt), was es Ihnen ermöglicht, eine Position im Diagramm zu betrachten, während Sie den folgenden Text lesen. Wenn Sie einen PostScript-Drucker besitzen, können Sie eine druckfertige PostScript-Datei (in einem ZIP-Archiv) herunterladen, welche das Diagramm auf einer einzelnen Seite Papier darstellt.
Ein Diagramm in einem neuen Browserfenster öffnen:
|
Das Diagramm repräsentiert die Spalten der Maschine, nachdem sie für die Berechnung von B2n-1 (für n=4) eingestellt wurden. Die nebenstehende Tabelle gewährt einen gleichzeitigen Blick auf all die aufeinander folgenden Änderungen, die diese Spalten während der Berechnung durchlaufen. (Wir verweisen den Leser für Erklärungen bezüglich der Art und der Notation solcher Tabellen auf Notiz D).
Sechs numerische Daten sind in diesem Fall als Vorgabe für die Kombinationen notwendig. Diese Daten sind 1, 2, n(=4), B1, B3 und B5. Wäre n=5, würde als zusätzliches Datum B7 benötigt; wäre n=6, benötigten wir auch B9 und so fort. Die tatsächlich benötigte Anzahl von Datenwerten ist immer n+2 und von diesen n+2 Daten sind immer ![]() aufeinander folgende Bernoulli-Zahlen. Der Grund, warum die als Daten vorgegebenen Bernoulli-Zahlen dennoch in den Ergebnis-Spalten im Diagramm eingetragen sind liegt darin, dass wir ohne weiteres annehmen können, wir hätten diese Zahlen zuvor von der Maschine selbst berechnen lassen, wobei jedes B zunächst als Ergebnis erscheint, bevor es bei der Berechnung des folgenden B als Datum genutzt wird. Dies ist also ein Beispiel für einen Fall (auf den in Notiz D angespielt wurde), in dem dieselben Variable mehr als eine Aufgabe in Folge erfüllen. Es ist wahr, dass wir, wenn wir unsere Berechnung von B7 vollständig isoliert betrachten, folgern könnten, dass B1,
B3 und B5 aus einer beliebigen Quelle in die Spalten gelangt sind und es wäre dann vielleicht sinnvoller, sie in den Spalten V4, V5 und V6 als Daten einzutragen, nicht als Ergebnisse. Wir nehmen jedoch nicht diesen Standpunkt ein. Im Gegenteil, wir nehmen an, dass die Maschine soeben dabei ist, die Bernoulli-Zahlen von Beginn an bis zu einer unbestimmten Anzahl zu berechnen und dass wir lediglich eine einzelne Berechnung aus der Abfolge der verschiedenen Serien von Berechnungen, welche die Maschine soeben durchführt, ausgewählt haben, um damit ein Beispiel zu zeigen. Für den Fall, dass die Bs Bruchzahlen sind, müssen wir wissen, dass sie als Dezimalbrüche berechnet und angezeigt werden. Dieser Umstand gilt im Übrigen für jegliche Berechnungen. In vielen der bereits gegebenen Beispiel in der Übersetzung und in den Notizen können einige der Daten, oder auch temporäre und endgültige Ergebnisse, genau so gut in Form von gebrochenen Zahlen erscheinen, wie als ganze Zahlen. Die Art der Prozesse bliebe dabei, da die Beispiele passend gewählt wurden, gegenüber dem Ablauf mit ganzen Zahlen unverändert.
aufeinander folgende Bernoulli-Zahlen. Der Grund, warum die als Daten vorgegebenen Bernoulli-Zahlen dennoch in den Ergebnis-Spalten im Diagramm eingetragen sind liegt darin, dass wir ohne weiteres annehmen können, wir hätten diese Zahlen zuvor von der Maschine selbst berechnen lassen, wobei jedes B zunächst als Ergebnis erscheint, bevor es bei der Berechnung des folgenden B als Datum genutzt wird. Dies ist also ein Beispiel für einen Fall (auf den in Notiz D angespielt wurde), in dem dieselben Variable mehr als eine Aufgabe in Folge erfüllen. Es ist wahr, dass wir, wenn wir unsere Berechnung von B7 vollständig isoliert betrachten, folgern könnten, dass B1,
B3 und B5 aus einer beliebigen Quelle in die Spalten gelangt sind und es wäre dann vielleicht sinnvoller, sie in den Spalten V4, V5 und V6 als Daten einzutragen, nicht als Ergebnisse. Wir nehmen jedoch nicht diesen Standpunkt ein. Im Gegenteil, wir nehmen an, dass die Maschine soeben dabei ist, die Bernoulli-Zahlen von Beginn an bis zu einer unbestimmten Anzahl zu berechnen und dass wir lediglich eine einzelne Berechnung aus der Abfolge der verschiedenen Serien von Berechnungen, welche die Maschine soeben durchführt, ausgewählt haben, um damit ein Beispiel zu zeigen. Für den Fall, dass die Bs Bruchzahlen sind, müssen wir wissen, dass sie als Dezimalbrüche berechnet und angezeigt werden. Dieser Umstand gilt im Übrigen für jegliche Berechnungen. In vielen der bereits gegebenen Beispiel in der Übersetzung und in den Notizen können einige der Daten, oder auch temporäre und endgültige Ergebnisse, genau so gut in Form von gebrochenen Zahlen erscheinen, wie als ganze Zahlen. Die Art der Prozesse bliebe dabei, da die Beispiele passend gewählt wurden, gegenüber dem Ablauf mit ganzen Zahlen unverändert.
In obiger Tabelle und im Diagramm beachten wir die Vorzeichen der Bs nicht weiter, sondern lediglich ihre numerische Größe. Die Maschine würde das Vorzeichen jeder Zahl natürlich korrekt angeben, aber wir können nicht auf jedes Detail dieser Art so weit eingehen, wie wir das vielleicht wünschen würden. Die Kreise für die Vorzeichen im Diagramm sind daher absichtlich leer gelassen.
Die Operations-Karten 1, 2, 3, 4, 5 und 6 bereiten ![]() vor. Karte 1 multipliziert folglich n mit zwei und die drei Ergebnis-Variablenkarten, die zu V4, V5 und V6 gehören, erlauben es das Ergebnis 2n in jeder dieser letztgenannten Spalten zu platzieren (in diesem Fall wird das Ergebnis dreifach in darauf folgenden Aufgaben benötigt). Wir sehen, dass die oberen Indices der während Operation 1 genutzten zwei Variablen unverändert bleiben.
vor. Karte 1 multipliziert folglich n mit zwei und die drei Ergebnis-Variablenkarten, die zu V4, V5 und V6 gehören, erlauben es das Ergebnis 2n in jeder dieser letztgenannten Spalten zu platzieren (in diesem Fall wird das Ergebnis dreifach in darauf folgenden Aufgaben benötigt). Wir sehen, dass die oberen Indices der während Operation 1 genutzten zwei Variablen unverändert bleiben.
Wir wollen nicht auf die Details jeder Operation einzeln eingehen, da die Tabelle und das Diagramm sie ausreichend beschreiben. Wir wollen lediglich einige, wenige besondere Fälle betrachten.
Durch die Operation 6 wird eine positive Größe in eine negative Größe umgewandelt, indem der Wert einfach von einer Spalte abgezogen wird, in der eine Null eingetragen ist. (Das Vorzeichen oberhalb von V8 würde bei diesem Ablauf zu − werden).
Die Operation 7 wird unverständlich sein, wenn wir uns nicht daran erinnern, dass wenn die Berechnung für n = 1 statt für n = 4 durchgeführt würde, die Operation 6 die Berechnung von B1 selbst bereits beendet hätte. Die Maschine würde in diesem Fall B1 in Spalte V21 eintragen und dann ganz anhalten, oder die Operationen 1, 2…7 mit dem nächsten Wert für n(=2) durchlaufen, um damit B3 zu berechnen (nachdem sie vor diesem Neustart die Zahl in Spalte V3, die das vorherige n=1 enthält, durch die Addition von eins zu zwei geändert hat). Nun muss Operation 7 entweder das Ergebnis Null haben (wenn n=1 ist), oder ein Ergebnis größer als Null, wie im gegenwärtigen Fall. Die Maschine folgt dem einen oder anderen der beiden soeben beschriebenen Wege, abhängig vom Ergebnis der Operation 7. Um die Notwendigkeit dieser experimentellen Operation zu verstehen ist es wichtig daran zu denken, worauf wir bereits zuvor hingewiesen haben: dass wir keine perfekt isolierte und unabhängige Berechnung betrachten, sondern eine einzelne aus einer Serie von vorausgehenden und nachfolgenden Berechnungen.
Die Karten 8, 9 und 10 liefern ![]() . In Operation 9 sehen wir ein Beispiel für einen oberen Index, der wieder einen Wert hat, nachdem er von einem vorherigen Wert auf Null geändert war. V11 war nacheinander 0V11, 1V11, 2V11, 0V11 und 3V11 und von der Art der Aufgabe her, die Spalte V11 in der Berechnung erfüllt, wird ihr Index weiterhin nach dem beschriebenen Schema, das bei genauer Betrachtung regulär und periodisch ist, wechseln.
. In Operation 9 sehen wir ein Beispiel für einen oberen Index, der wieder einen Wert hat, nachdem er von einem vorherigen Wert auf Null geändert war. V11 war nacheinander 0V11, 1V11, 2V11, 0V11 und 3V11 und von der Art der Aufgabe her, die Spalte V11 in der Berechnung erfüllt, wird ihr Index weiterhin nach dem beschriebenen Schema, das bei genauer Betrachtung regulär und periodisch ist, wechseln.
Karte 12 erfüllt dieselbe Aufgabe wie Karte 7 im vorigen Abschnitt, da, falls n =2 wäre, mit der 11. Operation die Berechnung von B3 beendet wäre.
Die Karten 13 bis 20 erzeugen A3. Da A2n-1 immer aus 2n-1 Faktoren besteht, hat A3 drei Faktoren und wir werden sehen, dass die Karten 13, 14, 15 und 16 den zweiten dieser Faktoren erzeugen und ihn mit dem ersten multiplizieren. Die Karten 17, 18, 19 und 20 erzeugen den dritten Faktor und multiplizieren ihn mit dem Produkt der zwei vorherigen Faktoren.
Karte 23 hat eine Aufgabe wie die Karten 11 und 7 zu erfüllen, da wenn n =3 wäre die 21. und 22. Operation die Berechnung von B5 vollendet hätte. Da unser Fall B7 ist, geht die Berechnung noch eine Stufe weiter und wir müssen nun die Aufmerksamkeit auf den Fakt lenken, dass es zur Berechnung von A7 lediglich nötig ist, die Gruppe der Operationen 13 bis 20 genau zu wiederholen und sodann, um die Berechnung von B7 zu beenden, die Operationen 21 und 22 nochmals auszuführen.
Wir sehen, dass jede Erhöhung von n in B2n-1 um Eins eine zusätzliche Wiederholung der Operationen (13…23) für die Berechnung von B2n-1 beinhaltet. Es sind diese Operationen nicht nur für jede solche Wiederholung exakt dieselben, sie werden auch mit Zahlen aus denselben Spalten versorgt, mit einer einzigen Ausnahme bei Operation 21, die natürlich nun B5 (aus V23) statt B3 (aus V22) benötigt. Diese Identität der Spalten, welche die benötigten Zahlen liefern darf nicht mit einer Identität der Werte verwechselt werden, die in diesen Spalten eingetragen sind und die sie an die Mühle geben. Die meisten dieser Werte erfahren eine Veränderung während eines Durchlaufs der Operationen (13…23) und folglich präsentieren die Spalten auch einen neuen Satz von Werten für die Bearbeitung beim nächsten Durchlauf von (13…23).
Nach der Beendigung der Wiederholung der Operationen (13…23) zur Berechnung von B7 sind die Änderungen der Werte der Variablen die folgenden
V6 = 2n-4 an Stelle von 2n-2. V7 = 6 . . . . . . . . . . . . . 4. V10 = 0 . . . . . . . . . . . . . 1. V13 = A0+A1B1+A3B3+A5B5 an Stelle von A0+A1B1+A3B3.
In diesem Zustand sind die noch verbleibenden Prozesse zunächst, den Wert aus Spalte V13 nach V24 zu übertragen, dann V6, V7 und V13 gleich Null zu setzen und zu V3 Eins zu addieren, womit die Maschine nun bereit dazu wäre, den Wert für B9 zu berechnen. Die Operationen 24 und 25 erfüllen diese Aufgabe. Man mag es für ungewöhnlich ansehen, dass die Operation 25 den oberen Index von V3 unverändert gleich Eins belässt, jedoch müssen wir uns daran erinnern, dass diese Indizes für jede Berechnung von vorne beginnen und dass Operation 25 in der Spalte V3 ja den ersten Wert für die neue Berechnung einträgt.
Es sollte auch klar sein, dass wenn die Gruppe (13…23) wiederholt wird, in einigen der oberen Indizes während dieser Wiederholung Veränderungen eintreten: zum Beispiel wird 3V6 geändert zu 4V6 und 5V6.
Wir sehen also, dass für n=1 neun, für n=2 vierzehn und für n>2 fünfundzwanzig Operationskarten benötigt werden, dass aber keine weiteren mehr benötigt werden, wie groß auch immer n werden mag. Nicht nur das, es sind diese selben fünfundzwanzig Karten auch ausreichend für die Berechnung aller Zahlen von B1 bis B2n-1 inklusive. Im Hinblick auf die Anzahl der Variablen-Karten erinnern wir uns, dass in vorherigen Notizen bereits erwähnt wurde, dass im Durchschnitt drei solcher Karten für jede Operation (nicht jedoch für jede Operations-Karte) als Bedarf geschätzt werden. Demgemäß wird die Berechnung von B1 siebenundzwanzig Variablenkarten benötigen, B3 zweiundvierzig solcher Karten, B5 fünfundsiebzig und für jedes weitere B nach B5 wären dreiunddreißig weitere Karten nötig (da jede Wiederholung der Gruppe (13…23) elf zu der Anzahl der für die Berechnung des vorherigen B benötigten Operationen hinzufügt). Wir müssen nun jedoch erklären, dass wann immer ein Zyklus von Operationen vorliegt, der lediglich mit Zahlen aus denselben Spalten versorgt wird und ebenso sein Ergebnis für jede Wiederholung der ganzen Gruppe in immer derselben Spalte ablegt, dieser Prozess einen Zyklus von Variablenkarten zur Erledigung seiner Aufgaben erlaubt. Es liegt offenbar viel mehr Symmetrie und es liegen einfachere Voraussetzungen vor, wenn ein Fall die Wiederholung sowohl der Variablen-, als auch der Operationskarten erlaubt. Unser gegenwärtiges Beispiel ist von dieser Art. Die einzige Abweichung von einer perfekten Identität in allen Prozessen und genutzten Spalten für jede Wiederholung der Operationen (13…23) liegt darin, dass Operation 21 immer einen ihrer Faktoren aus einer neuen Spalte benötigt und dass Operation 24 ihr Ergebnis immer in eine neue Spalte einträgt. Da diese Variationen jedoch bei jeder Wiederholung derselben Gesetzmäßigkeit folgen (Operation 21 benötigt einen Faktor immer aus einer Spalte, die um eins höher ist als die beim vorherigen Durchlauf und Operation 24 schreibt ihr Ergebnis immer in eine Spalte, die um eins höher ist als jene, welche das vorige Ergebnis erhielt), kann man sie leicht durch eine passende Auswahl der Variablenkarten in der wiederkehrenden Gruppe (oder dem Zyklus) erreichen.
Wir können noch anmerken, dass die durchschnittliche Schätzung von drei Variablenkarten, die für jede Operation gebraucht werden, nicht als absoluter und wörtlich zu nehmender Wert für alle Fälle um Umstände gesehen werden soll. Viele spezielle Umstände, die entweder in der Natur des Problems liegen oder in den Einstellungen der Maschine für bestimmte Eventualitäten, beeinflussen und verändern diesen Durchschnitt mehr oder weniger stark. Es bleibt jedoch eine sichere und korrekte allgemeine Regel für die Abschätzung. Im vorhergehenden Fall gibt sie uns fünfundsiebzig Variablenkarten als Gesamtanzahl der benötigten Karten für die Berechnung jeden Bs nach B3 an. Dies liegt sehr nahe an der tatsächlichen Anzahl, die in der Praxis benötigt wird, jedoch können wir hier nicht auf die Einzelheiten der wenigen speziellen Umstände in diesem Beispiel eingehen (die es tatsächlich in der einen oder andere Phase vermutlich fast jeder Berechnung gibt), welche diese Zahl minimal verändern.
Es ist offensichtlich, dass dieselben fünfundsiebzig Variablenkarten für die Berechnung jeder folgenden Zahl wiederholt werden können, genau nach demselben Prinzip, das die Wiederholung der dreiunddreissig Variablenkarten der Operationen (13…23) bei der Berechnung jeder einzelnen Zahl erlaubt. Es wird also einen Zyklus eines Zyklus von Variablenkarten geben.
Wenn wir nun die Notationen für Zyklen anwenden, wie sie in Notiz E erklärt wurde, können wir die Operationen für die Berechnung der Bernoulli-Zahlen in der folgenden Weise angeben:—

Schließlich repräsentiert
die Gesamtzahl der Operationen die notwendig wäre, um jede Bernoulli-Zahl von B1 bis B2n-1 inklusive zu berechnen.
In dieser Formel sehen wir einen variierenden Zyklus von erster Ordnung und einen gewöhnlichen Zyklus von zweiter Ordnung. Letzterer ist in diesem Fall im variierenden Zyklus enthalten.
Wenn wir die zehn Arbeitsvariablen des Diagramms betrachten sehen wir, dass obwohl der Wert jede dieser Variablen (außer V4 und V5) eine Reihe von Veränderungen durchläuft, während ihre jeweilige Aufgabe in dieser Berechnung festliegt und unveränderlich ist. So dient V6 immer dazu, die Zähler der Faktoren für jedes A vorzubereiten, V7 die Nenner. V8 wird immer der (2n-3)te Faktor von A2n-1 zugewiesen und V9 der (2n-1)te. V10 entscheidet immer, welchen von zwei Wegen die darauf folgenden Prozesse durchlaufen, indem es den Wert von n durch eine Subtraktion testet. Auf die weiteren Variablen gehen wir nicht mehr ein. Es ist bei allen Berechnungen wünschenswert, die Prozesse so zu arrangieren, dass die Aufgaben, die von den Variablen erfüllt werden, so einheitlich und festgelegt wie möglich bleiben.
Wenn wir annehmen, wir wollten nicht nur B1, B3, &c. tabellieren, sondern ebenso A0, A1, &c., dann müssten wir lediglich eine weitere Serie von Variablen V41, V42, &c. für den Empfang letzterer Ergebnisse zuweisen, die immer in V11 erscheinen. Wir könnten stattdessen, oder auch zusätzlich zu dieser zweiten Serie von Ergebnissen, den Werte jedes aufeinander folgenden Gesamt-Terms der Serie (8.), also A0, A1B1, A3B3, &c. tabellieren. Wir müssten dazu lediglich jedes B mit seinem zugehörigen gerade berechneten A multiplizieren und diese aufeinander folgenden Produkte in dafür ausgewählte Ergebnisspalten platzieren.
Die Gleichung (8.) ist auch von einem anderen Standpunkt aus noch interessant. Sie stellt einen speziellen Fall des allgemeinen Integrals der folgenden Gleichung von uneinheitlichen Differenzen dar:—
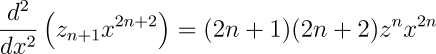
für bestimmte spezielle Voraussetzungen für z, x und n.
Das allgemeine Integral selbst ist von der Form
und es ist einen Hinweis wert, das die Maschine (in einer der vorangegangenen sehr ähnlichen Weise) den Wert dieser Gleichung für die meisten anderen Annahmen für die Funktionen im Integral genauso leicht oder (in vielen Fällen) noch leichter berechnen kann, als die Gleichung (8.).
A.A.L.
Diese Bemerkung scheint weitergehender Kommentierung zu bedürfen, da sie in gewissem Grade darauf abzielt, den Geist durch einen Widerspruch zum folgenden Absatz aufzurühren, in welchem erläutert wird, wie die Maschine mit nur vier Grundrechenarten tatsächlich jede Art von Berechnung durchführen kann. Die Diskrepanz tritt zudem in der Übersetzung deutlicher zu Tage als im Original, da es unmöglich ist, die mit den Möglichkeiten der Französischen Sprache gegebenen Feinheiten der Phrasen dieser beiden Absätze eben so gut in der Englischen Sprache wiederzugeben [Anm. d. Übers. Man bedenke nun die zusätzlichen Verluste bei der neuerlichen Übersetzung vom Englischen ins Deutsche]. Die Erklärung liegt hierin: Im ersten Fall ist die Ausführung dieser vier Operationen der fundamentale Startpunkt und das als Aufgabe der Maschine angesehene Ziel ist die nachfolgende Kombination dieser Operationen in jeder denkbaren Zusammenstellung, während im anderen Fall die Ausführung einer einzigen der vier Operationen, je nach Lust und Laune ausgewählt, bereits das ultimativ einzige und letzte Ergebnis der dieser Maschine aufgegebenen Rechnung ist, welches danach nicht in irgendeiner Weise weiter verwendet oder kombiniert werden kann. Die eine Maschine beginnt dort, wo die andere endet. Sollte diese Unterscheidung nun nicht vollkommen klar geworden sein, wird sie es beim weiteren Lesen der Denkschrift und der angehängten Notizen werden.—NOTIZ DES ÜBERSETZERS.
Die Idee, dass die eine Maschine ein Nachkomme der anderen sei, erscheint als natürliche und plausible Annahme, bis eine Überlegung uns daran erinnert, dass keine notwendige Folge oder Verbindung zwischen zwei solchen Erfindungen bestehen muss und dass sie gänzlich unabhängig voneinander sein können. L. M. Menabrea teilt diese Vorstellung mit Personen, die nicht seine profunde und akkurate Einsicht in die Natur beider Maschinen haben. In Notiz A (in den Notizen im Anhang der Denkschrift) wird jedoch ausführlich genug dargelegt, dass diese Annahme unbegründet ist. L. M. Menabreas Möglichkeiten waren keineswegs so gelagert, dass er Informationen zu diesem selbstverständlich und geradezu unbewusst vermuteten Punkt erlangt hätte, die kaum einer Klärung bedurft hätten.—NOTIZ DES ÜBERSETZERS.
Dies sollte in nicht zu unqualifizierter Weise verstanden werden. Die Maschine ist unter bestimmten Umständen in der Lage heraus zu fühlen, welche von zwei oder mehr möglichen Eventualitäten aufgetreten ist und daraufhin den zukünftigen zu gehenden Weg auszurichten.—NOTIZ DES ÜBERSETZERS.
Wenn eine Zahl in die Mühle übertragen wird, wird sie nicht immer durch die Null ersetzt. Dies wird in einem späteren Abschnitt der Denkschrift erläutert, sowie in allen Details in Notiz D.—NOTIZ DES ÜBERSETZERS.
Da sich keine Gelegenheit bot, mit Mr. Babbage über die Art und Weise weise zu diskutieren, in der das Kombinieren von algebraischen Vorzeichen in seiner Maschine behandelt wird, gebe ich hier nicht vor, die von ihm angewandte Methode vorzustellen. Ich dachte mir, es sei notwendig dieses im ursprünglichen Artikel fehlende Detail auszufüllen, da der Text ohne die Erwähnung wenigstens einer Möglichkeit zur Lösung dieses essenziellen Teils des fraglichen Problems nicht perfekt wäre.
Für eine Erklärung der oben links an den "V"s angeschriebenen Indizes in dieser sowie der vorhergehenden Tabelle müssen wir den Leser auf Notiz D verweisen, die im Anhang der Denkschrift zu finden ist.—NOTIZ DES ÜBERSETZERS.
Dieser Satz ist in der Übersetzung leicht abgeändert, um den derzeitigen Stand der Maschine genauer wiederzugeben.—NOTIZ DES ÜBERSETZERS.
Die hier angedeutete Notation ist ein sehr interessantes und wichtiges Thema und hätte sehr wohl eine eigene und detaillierte Notiz im Anhang der Denkschrift verdient. Im Rahmen des vorgesehenen Umfangs war es aber unmöglich, ein so weites Feld auch nur anzuschneiden.—NOTIZ DES ÜBERSETZERS.
Wir wollen damit nicht sagen, dass die einzige Verwendung der Jacquard-Karten die der Steuerung von algebraischen Operationen ist. Wir wollten vielmehr erklären, dass die Karten und Teile des Mechanismus, die diese Operationen steuern, völlig unabhängig von denen sind, die für andere Zwecke benötigt werden. L. M. Menabrea erläutert, dass es bei der Maschine drei Klassen von Karten für drei verschieden Gruppen von Objekten gibt, als da wären Operations-Karten, Variablen-Karten und spezielle Zahlen-Karten.
Tatsächlich wäre eine solche Erweiterung, wie wir sie erwähnen, lediglich eine weitere und perfektere Entwicklung eines beliebigen Systems zur treffenden Behandlung der Vorzeichen Plus und Minus. Wie gekonnt schon L. M. Menabrea diesen Teilbereich angeschnitten hat, ist in Notiz B aufgezeigt.
Die Maschine hätte auch für Tabellierungen mit einem größeren Wert für n als sieben konstruiert werden können. Da aber jede weitere zu n hinzugefügte Einheit den Umfang des notwendig werdenden Mechanismus vergrößert, wäre aus diesem Grund eine Grenze gegeben, jenseits der er praktisch nicht mehr realisierbar wäre. Sieben ist ausreichend groß für die Berechnung aller gewöhnlichen Tabellen.
Der Fakt, dass bei der Analytischen Maschine ein Mechanismus gleichen Umfangs ausreichend ist, um Lösungen von ![]() zu erhalten, ganz gleich ob n=7, n=100.000 oder n=eine beliebige Zahl ist, legt direkt nahe, wie gänzlich andersartig die Natur der Prinzipien sein muss, durch deren Anwendung die Geräte jeweils in die Lage versetzt werden, die Arbeitsabläufe abstrakter geistiger Operationen auszuführen und dass dies im Falle der Analytischen Maschine zudem offensichtlich die Annahme voraussetzt, dass diese die Prinzipien nicht nur in höherwertigen und dichteren Beschreibung beinhaltet als die Differenzmaschine, sondern dass dabei zugleich auch der praktische Wert der Maschine, deren Grundlage sie ausmachen, stark erweitert wird.
zu erhalten, ganz gleich ob n=7, n=100.000 oder n=eine beliebige Zahl ist, legt direkt nahe, wie gänzlich andersartig die Natur der Prinzipien sein muss, durch deren Anwendung die Geräte jeweils in die Lage versetzt werden, die Arbeitsabläufe abstrakter geistiger Operationen auszuführen und dass dies im Falle der Analytischen Maschine zudem offensichtlich die Annahme voraussetzt, dass diese die Prinzipien nicht nur in höherwertigen und dichteren Beschreibung beinhaltet als die Differenzmaschine, sondern dass dabei zugleich auch der praktische Wert der Maschine, deren Grundlage sie ausmachen, stark erweitert wird.
Eine ausführlichere Beschreibung der Methode, mit der Vorzeichen behandelt werden ist in L. M. Menabreas Denkschrift enthalten. Er äußerte Zweifel (in einer seiner Notizen), ob er selbst die tatsächlich angewandten Methoden exakt getroffen habe — seine Erklärung stelle lediglich eine Vermutung dar. Dass diese Vermutung tatsächlich präzise mit den Fakten übereinstimmt, ist ein bemerkenswerter Umstand und kann als überzeugender Beleg dafür angesehen werden, wie tief greifend L. M. Menabrea vom wahren Geist der Erfindung inspiriert war. In der Tat ist die ganze Denkschrift eine bemerkenswerte Leistung wenn wir bedenken, dass L. M. Menabrea nur sehr wenige Möglichkeiten für den Zugriff auf adäquate Ideen im Bezug auf die Analytische Maschine zur Verfügung standen. Es erfordert allerdings eine beachtliche Vertrautheit mit der abstrusen und komplizierten Natur eines solchen Fachgebietes, um das tiefe Eindringen des mit so geringen Möglichkeiten ausgestatteten Autors in solch angemessener und verständiger Weise würdigen zu können.
Diese Einstellung wird nur händisch vorgenommen.
Die Kreise wegzulassen ist bequemer, wenn die Vorzeichen + oder − dargestellt werden sollen.
Wir empfehlen dem Leser, die aufeinander folgenden Ersetzung in L. M. Menabreas Tabelle rückwärts von (1) bis (4) zu verfolgen. Dies ist leicht möglich durch die oberen und unteren Indizes und es ist interessant zu beobachten, wie sich ein V nach dem anderen (sozusagen) in zwei andere Vs in einer anderen Spalte der Tabelle verästelt, bis am Ende die Vs der ursprünglichen Daten erreicht sind.
Diese Division würde ausgeführt, indem die Zahl 2 auf jeder neuen Spalte erschiene, welche für diesen Zweck geeignet wäre, um sodann diese Spalte (die im strengsten Sinne eine Arbeits-Variable darstellt) sich selbst nacheinander durch V32, V33, &c. dividieren zu lassen.
Es ist zu sehen, dass wenn statt nur vier Termen auch der Rest des Faktors (A + A cos ![]() + &c.) berücksichtigt würde, sich für C3 der zusätzliche Term ½B1A4 ergäbe und für C4 die zwei Terme BA4 sowie ½B1A5. Dies wäre in der Tat auch dann der Fall gewesen, wenn eben sechs Terme multipliziert worden wären.
+ &c.) berücksichtigt würde, sich für C3 der zusätzliche Term ½B1A4 ergäbe und für C4 die zwei Terme BA4 sowie ½B1A5. Dies wäre in der Tat auch dann der Fall gewesen, wenn eben sechs Terme multipliziert worden wären.
Ein Zyklus, der n weitere Zyklen enthält, die jeweils innerhalb des vorhergehenden liegen, wird als Zyklus n+1ter Ordnung bezeichnet. Ein Zyklus kann viele weitere Zyklen enthalten und dennoch nur ein Zyklus zweiter Ordnung sein. Wenn eine Serie für eine Anzahl von Termen einem bestimmten Gesetz folgt und ein nächstes Gesetz für eine weitere Anzahl von Termen folgt, dann gibt es einen Zyklus von Operationen für jedes neue Gesetz, doch ein neuer Zyklus liegt nicht innerhalb des vorherigen, vielmehr folgt einer auf den anderen. Daher kann ihre Anzahl unendlich sein, ohne dass sie die Ordnung des Zyklus verändern, der eine Wiederholung einer solchen Serie enthält.
Die Maschine kann natürlich nur in dieser Weise Grenzwerte für einfache und ungebundene Funktionen errechnen. Es ist offensichtlich, dass sie lediglich den Umgang mit endlichen Werten ermöglicht und dass daher jegliche Berechnung von Grenzwerten (oder anderen Funktionen), die direkt von der Einführung undefinierter Werte für das Erhöhen oder Verringern von Variablen abhängen, absolut jenseits des Rahmens ihrer Leistungsfähigkeit liegt. Ihre Bauweise und ihre Konstruktion sind bemerkenswert gut darauf angepasst, alle endlichen Erhöhungen oder Verringerungen von Variablen (wie klein oder groß auch immer sie seien) zu berücksichtigen und die richtigen und logischen Modifikationen der Form oder des Wertes der von diesen Variablen abhängenden Differenzen zu entwickeln. Die Maschine kann so gesehen den kompletten Kalkulus der finiten Differenzen abdecken, welcher viele Theoreme beinhaltet, die speziell und wunderbar geeignet sind mit ihren Methoden entwickelt zu werden und hierzu besonders interessante Denkanstöße zu liefern. Wir können als ein Beispiel dafür die Berechnung der Bernoulli-Zahlen mit der Methode der Null-Differenzen erwähnen.
Es ist interessant zu beobachten, dass ein so komplizierter Fall wie die Berechnung der Bernoulli-Zahlen dennoch in einem Punkt bemerkenswert einfach ist, nämlich dem, dass zur Berechnung von Millionen dieser Zahlen keine weitere Änderung der Einstellungen nötig ist, außer dem oben beschriebenen, einfachen Vorgang, der eine bestimmte Variable periodisch um einen fixen Wert erhöht.