Mondrian Blocks
Der Aufbau des Spiels
Mondrian Blocks ® ist ein typisches Legespiel. Es
besteht aus einem leeren Feld der Grösse 8 x 8, in das zunächst drei schwarze
Steine mit den Grössen 1x1, 1x2 und
1x3
gelegt werden. Sodann müssen die restlichen 8 farbigen
Steine hinzugefügt werden. Diese besitzen die Grössen 2x2,
2x3, 3x3, 4x1, 4x2,
4x3, 5x1 und 5x2.
 |
Die Packanord- nung der Edition weiss |
Die Position der drei schwarzen Steine am Anfang wird entweder einer
der beiliegenden 4x22 Karten entnommen oder ist frei gewählt.
Es werden vier sog. Editionen des Spieles angeboten: weiss (white),
blau (blue),
rot (red), gelb (yellow). Sie enthalten die gleichen schwarzen Steine
und
unterscheiden sich nur in den Farben der übrigen Steine.
Fertige Zusammenstellungen ähneln den grafischen Werken des
niederländischen Malers Piet Mondrian, (1872 - 1944),
daher der Name.
Das Spiel ist relativ neu, es erschien 2019 oder 2020 und gewann mehrere Preise. Zum Markenschutz s. Lit. [1].
| Das Spiel darf nicht
verwechselt werden mit dem sog. Mondrian
Art Problem.
Hierbei muss ein Quadrat in nicht kongruente Rechtecke geteilt werden,
sodass die Fläche des grössten Steins minus die Fläche des kleinsten
Steins ein Minimum wird (Was sich Menschen alles ausdenken...) Für ein
8 x 8 Feld beträgt dieser Wert 6, weit entfernt von den Mondrian
Blocks. mit 11. |
Lösungen
Für dieses Legespiel habe ich ein Programm geschrieben, das zunächst
eine freie Vorgabe der Positionen der drei schwarzen Steine ermöglicht
und dann dazu alle Lösungen mit den übrigen Steinen bestimmt.
Einige Erkenntnisse hierzu:
Auf der Webseite des Spiels [2] wird angegeben, dass jede der 88
beigelegten Karten zu jeweils nur einer Lösung führt. Für 10 Karten,
die ich bisher
ausprobiert habe, ist das auch richtig. Für den Test aller Karten hatte
ich noch keine
Zeit. Worin dann die angeblich unterschiedlichen Anforderungen der
Karten bestehen sollen bleibt unklar.
Lösungen für vorgegebene Ausgangsstellungen auf den Karten gebe ich hier nicht, damit der Spielspass erhalten bleibt.
Andere selbst angenommene Anfangsstellungen führen zu ganz unterschiedlichen Ergebnissen. Vier Beispiele hierzu:
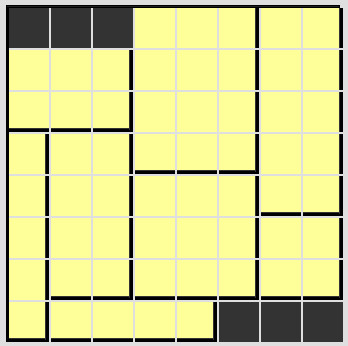 |
 |
|
548
Lösungen, mit der Rotationssymmetrie 180° noch 274 Lösungen mit
unterschiedlichen Relativpositionen.
Das Bild zeigt eine davon. |
Keine Lösung |
Da sich alle Steine in ihren Abmessungen unterscheiden ist es nicht
nötig, sie in der grafischen Darstellung einer Lösung zusätzlich farbig
zu
kennzeichnen.
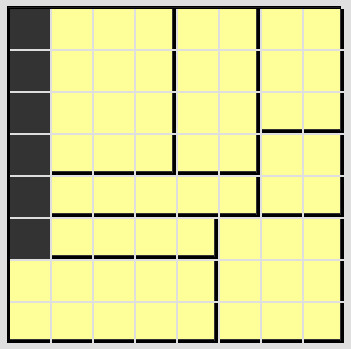 |
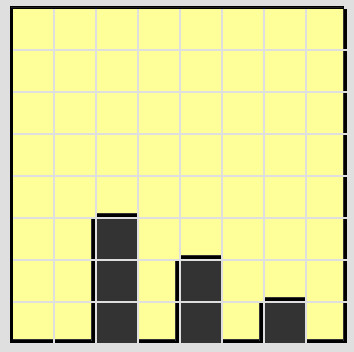 |
|
468 Lösungen. |
Keine Lösung |
Das Spiel ist in zweifacher Hinsicht herausfordernd: zu den
Vorgaben auf
den Karten ist bekannt, dass eine Lösung existiert.Man muss nur lange
genug suchen. Eigene Vorgaben hingegen bleiben unbestimmt. Sofern
mehrere Lösungen existieren, sind sie leicht zu finden. Eine genügt um
die Lösbarkeit zu beweisen.
Existiert keine
Lösung dann ist das nur durch Ausprobieren, soll heissen schwer bis
unmöglich nachzuweisen.
Literatur, Webseiten
[1] ![]() Markenschutz
Markenschutz
[2] Webseite des Spiels
[3]
xxx