Pentomino
Der Ausgangspunkt
Unter einem Pentomino
versteht man die Zusammenstellung von fünf (griech. penta)
gleich grossen Quadraten, die an ihren Kanten verbunden sind [2a].
Selten findet man die holprige deutsche Bezeichnung Quadratfünfling.
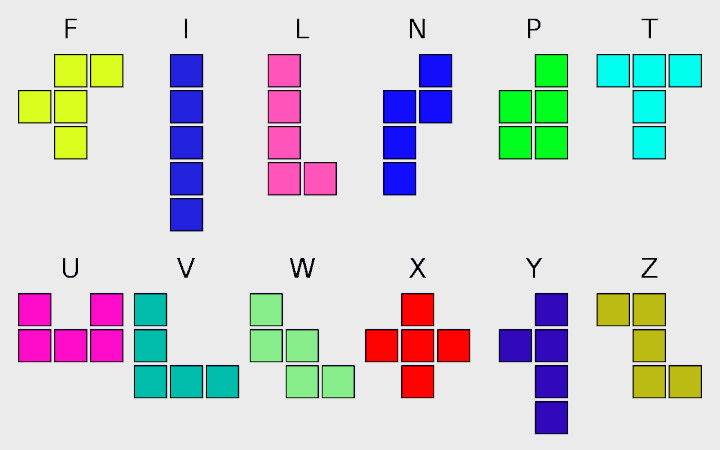
Es gibt 12 unterschiedliche Pentominos, sie sind mit dem Buchstaben
benannt, dem sie ähneln.
 |
|
alle 12 Pentominos |
Pentominos gehören zu den Polyominos
[1b], das sind Zusammenstellungen von zwei und mehr Quadraten.[2b]
Eingehend mit Polyominos befasst hat sich S.W. Golomb [1a], der auch
den Namen Pentomino gebrauchte.
Mit Pentomino kann nicht nur ein einzelner Stein, sondern daüber
hinaus eine Zusammenstellung der zwölf Steine zu einem Legespiel
gemeint sein. Die deutsche Bezeichnung ist zuweilen Zwölfer-Puzzle oder
Zwölfer-Spiel.
Die Steine sind flach ausgeführt oder aus Würfeln zusammen gesetzt.
Würfel erleichtern die Handhabung und bringen eine noch
schwierigere Klasse von Puzzles, nämlich die
dreidimensionalen, mit sich. Bis auf weiteres beschränke ich mich hier
auf die zweidimensionale Variante.
Mit den Steinen des Legespiels sollen vorgegebene zweidimensionale
Figuren gelegt werden. Andere Spieler versuchen die Frage zu
beantworten, wieviele unterschiedliche Lösungen eine Figur besitzt.
Eine
zuverlässige Antwort kann nur ein für diese Aufgabe geschriebenes
Programm geben. Im Folgenden einige Beispiele und Lösungen.
zweidimensionale Lösungen
Es versteht sich von selbst, dass eine Figur, die mit Pentominos
gelegt werden soll,
ein Vielfaches von 5 Feldern enthalten muss, maximal 5 x 12 = 60 Felder.
![]() Beispiel 1:
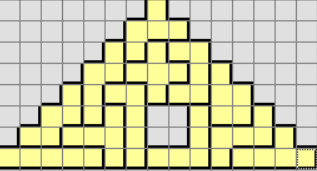
Beispiel 1:
 |
|
46 Lösungen, alle in P01-L46.txt |
![]() Beispiel 2:
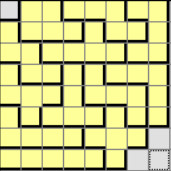
Beispiel 2:
 |
|
13752 Lösungen, alle in P02-L13752.txt |
![]() Beispiel 3:
Beispiel 3:
 |
|
44 Lösungen, alle in P03-L44.txt |
![]() Beispiel 4:
Beispiel 4:
 |
|
8 (2) Lösungen, alle in P04-L8.txt |
Eine Ergänzung zu den Lösungen in diesem Beispiel:
sofern die Figur unsymmetrisch ist, wiederholen sich die Lösungen
nicht.
Bei dreh- und spiegelsymmetrischen Figuren ist das anders. In ihnen
kann man manche Lösungen mittels Drehen oder Spiegeln ineinander
überführen, im Beispiel des Rechtecks 3 x 20 entstehen so 2 Gruppen
zu je vier. Innerhalb jeder Gruppe bleiben die Relativpositionen der
Steine
zueinander gleich. Ob man solche Lösungen mitzählt oder nur die sog.
"echten"
sei dahingestellt.
![]() Sehr viel mehr Vorlagen findet man u. a.
bei [2] und [3]
Sehr viel mehr Vorlagen findet man u. a.
bei [2] und [3]
dreidimensionale Lösungen
erscheinen hier in einer zukünftigen Bearbeitung.
Literatur, Webseiten
[1a] Golomb, Solomon W. : Polyominoes. Puzzles, Patterns, Problems, and Packings. 2. erw. Aufl..1994
[1b] Koth, Maria: Pentominos -
Figuren aus 5 Quadraten, o.J. online
[2a] Wikipedia Pentomino
[2b] Wikipedia Polyomino
[2c] Mathematische Basteleien Pentominoes
[2d] Pentoma
[3] Gerard's Universal Polyomino Solver
[4]
xxx