| |
Katalog: |
|
| |
|
|
 |
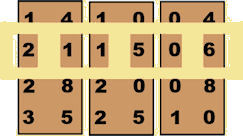
Historische Einmaleinstafeln
Historical Multiplication Tables up to ten
 Ansicht, view Ansicht, view
|
 |
| |
|
|
 |
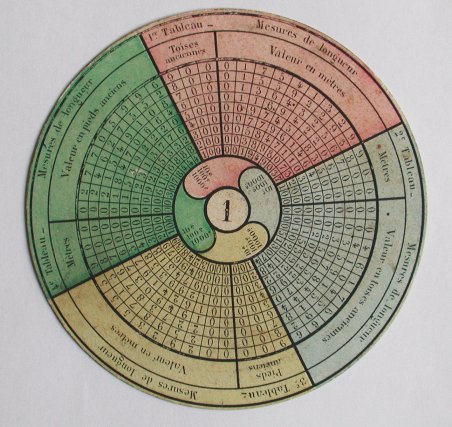
Multiplizierscheibe, Anfang 17. Jhd.
Disk for Multiplying, begin of 17th C.
 Ansicht, view Ansicht, view |
|
|
|
|
 |
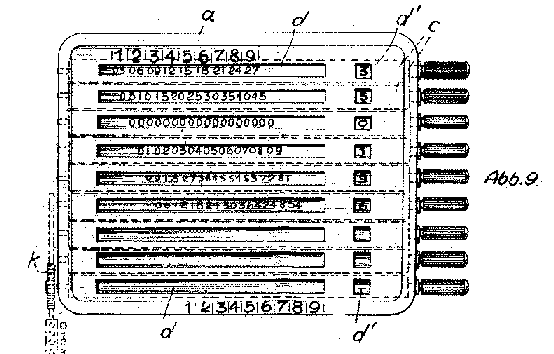
Fundamentalis Tabula Arithmeticae,
Deutschland
1638
Ansicht, view |
 |
|
|
|
 |
'Instrument for Arithmetic'
(arithmetical compendium)
England, 1667
Ansicht, view
|
 |
|
|
|
 |
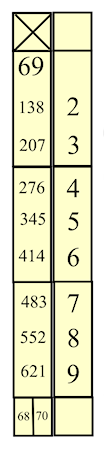
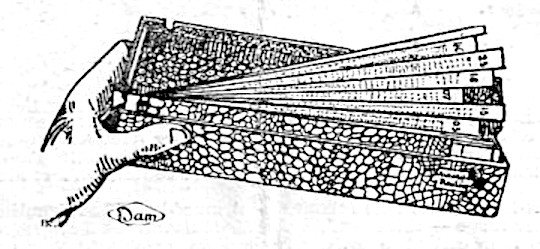
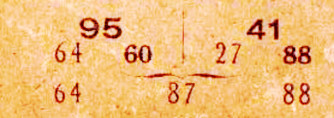
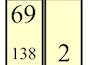
Multiplizierstäbe für zweistellige Zahlen, 1760
Rods for Multiplying two-digit Numbers, 1760
Ansicht, view |
 |
|
|
|
 |
Zahl-Buechlein, Deutschland 1776
Buch mit Multipliziertafeln fuer Preise und Zahlen
Zahl-Buechlein (in free translation 'small book with numbers'),
Germany 1776
Book with multiplying tables for prices and numbers
Ansicht, view
|
 |
| |
|
|
 |
Sehr viel mehr über Multipliziertafeln finden Sie in einem Artikel
im Abschnitt Publikationen oder in meinem Betrag im Rechnerlexikon
Much more about multiplication tables you will find in an article
in section Publications or in my contribution at Rechnerlexikon |
|
|
|
|
 |
Rechenscheibe von Grüson,
Deutschland 1790
Grueson's Calculating Disk,
Germany 1790
beschrieben bei  Publikationen Publikationen
described at  Publications Publications |
 |
|
|
|
 |
'Prompt Calculateur' von Maurand
Frankreich 1865
'Prompt Calculateur' by Maurand
France 1865
Ansicht, view
|
 |
| |
|
|
 |
Rechenmaschine von Esersky, 1874
Calculating machine by Esersky, 1874
 Rechnerlexikon Rechnerlexikon |
 |
|
|
|
 |
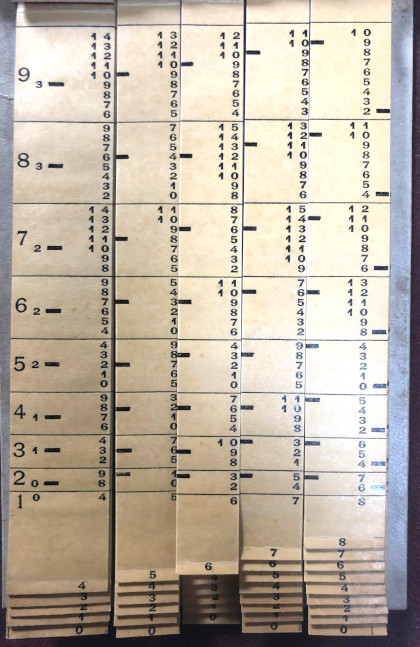
Die Multiplizierstäbe von Genaille und Lucas,
Frankreich, 1885
The Genaille-Lucas Rulers for Multiplication,
France, 1885
Ansicht, view
|
 |
|
|
|
 |
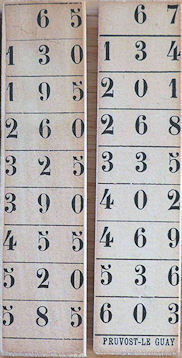
Die Rechenstäbchen von Pruvost Le Guay
Frankreich 1890
The Calculating Rods by Pruvost Le Guay
France 1890
Ansicht, view
|
 |
|
|
|
 |
Automultiplicateur Eggis
Schweiz, 1892
Switzerland, 1892
Ansicht, view |
 |
|
|
|
 |
Multiplicateur Barit, Frankreich, kurz nach 1900
Multiplicateur Barit, France, shortly after 1900
Ansicht, view |
 |
|
|
|
 |
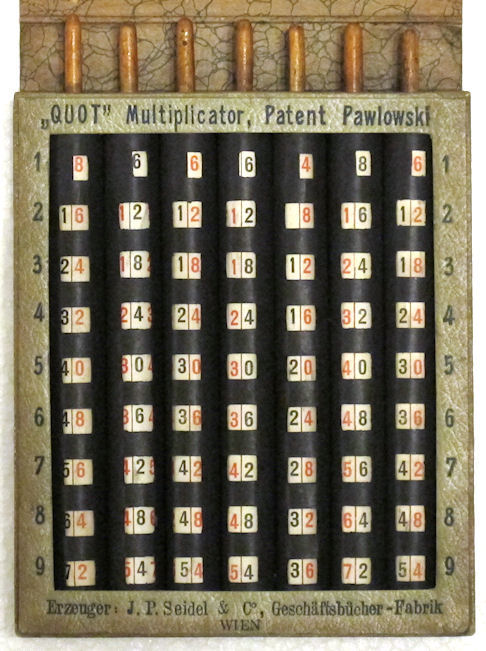
Quot Multiplicator, Österreich, um 1910
Quot Multiplicator, Austria, about 1910
Ansicht, view
|
 |
|
|
|
 |
Rechenschieber Faber 366, System Schumacher
Deutschland 1909
Slide Rule Faber 366, System Schumacher
Germany 1909
Ansicht, view |
 |
|
|
|
 |
'Rechenapparat Thesaurus', Deutschland, 1905
'Apparatus for Calculating Thesaurus', Germany, 1905
Ansicht, view |
|
|
|
|
 |
'Moltiplicatrice Utilis'
Italien, frühes 20. Jahrhundert
'Moltiplicatrice Utilis'
Italy, early 20th century
Ansicht, view
|
 |
|
|
|
 |
L'Auto-Calcul Roulois
Frankreich 1924
France 1924
Ansicht, view |
 |
|
|
|
 |
Multiplizierzylinder 'AMSA-Kalkulator',
Österreich, Anfang 20. Jhd.
Cylinder for Multiplication 'AMSA-Kalkulator',
Austria, begin of 20th c.
Ansicht, view |
 |
| |
|
|
 |
Rechengerät 'Multirex', Deutschland, Anfang 20. Jhd.
zum multiplizieren mehrstelliger Zahlen
Calculating device 'Multirex', Germany, begin of 20th c.
to multiply multi-digit numbers
 für eine Beschreibung gehen
Sie bitte zum Rechnerlexikon für eine Beschreibung gehen
Sie bitte zum Rechnerlexikon
for a description please go to Rechnerlexikon |
 |
|
|
|
 |
Rechengerät 'La Multi', Frankreich, ca. 1920
zum multiplizieren mehrstelliger Zahlen
Calculating device 'La Multi', France, about 1920
to multiply multi-digit numbers
 für eine Beschreibung gehen Sie bitte zum Rechnerlexikon für eine Beschreibung gehen Sie bitte zum Rechnerlexikon
for a description please go to Rechnerlexikon
 Funktionsmodell Funktionsmodell
working
model |
 |
| |
|
|
 |
Multiplizierhilfe 'Quick Multiplikator', Deutschland, um 1920
zum multiplizieren mehrstelliger Zahlen
und frühere Entwürfe
Aid for Multiplying 'Quick Multiplikator', Germany, about 1920
to multiply multi-digit numbers
and earlier designs
Ansicht, view
|
 |
| |
|
|
 |
Multiplizierhilfe 'Le Muldivi', Frankreich, um 1926
zum multiplizieren mehrstelliger Zahlen mit einer einstelligen
Aid for Multiplying 'Le Muldivi', France, about 1926
to multiply multi-digit numbers with single digit
Ansicht, view |
 |
| |
|
|
 |
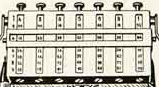
Rechenapparat Addor, Deutschland, 1927
zum Ablesen von Vielfachen bis 9999
Instrument for Calculation Addor, Germany, 1927
for reading multiples up to 9999
Ansicht, view
|
 |
| |
|
|
 |
Multiplizierhilfe 'Correnta-Roll' für den Zahlenschieber CBR.
Deutschland, um 1928
Aid for Multiplying 'Quick Multiplikator' for slide adder CBR.
Germany, about 1928
Ansicht, view |
 |
| |
|
|
 |
Bretter- und Kantholzrechenapparat 'Cubo'
Deutschland, ab 1927
Calculating device for timber 'Cubo'
Germany, from 1927 on
Ansicht, view
|
|